Tiger Lily Chess
External image links detected!
You know what would look worse on your page than this big, ugly warning? Broken image links. If you're the author, please make sure that doesn't happen to this page by replacing the following external graphic images with local copies.
Array
(
[0] => http://k9.eml.cc/cv/tlcsmall.png
)
 This variant sees my return to boards with
unusual hexagonal tessellations, this one inspired by the beauty of the
tiger lily.
This variant sees my return to boards with
unusual hexagonal tessellations, this one inspired by the beauty of the
tiger lily.
The board is constructed from hexagons with sides of equal length having 2 opposite internal angles of 60 degrees, the remaining
4 internal angles being 150 degrees each.
There are 72 such hexagons in total arranged to reflect the six-fold symmetry of the tiger lily and divided into 3 coloured sets of 24 hexagons each.
Setup

|

|

|
Each player starts with 18 pieces: 9 pawns, 3 bishops, 2 knights, 2 rooks, 1 queen and 1 king. The starting piece density is thus 50%, the same as FIDE-chess.
The starting position is shown on the image above left. The board is formed from 12 petals (6 inner and 6 outer), each of six hexagons. This is demonstrated in the image above top-right with the inner six petals white and the outer six petals black.
The coordinate system for the tiger lily board is illustrated in the image above bottom-right. The inner petals are labeled clockwise a-f, while the outer are labeled g-l. The hexagons within each petal are numbered 1-6, beginning in the center and working outwards and clockwise.
Pieces
| Name
|
Description
|
|
| King
|
Moves 1-step orthogonally or
diagonally. There is no castling.
Orthogonal moves cross edges or sides. In the image on the right the King's possible orthogonal moves are indicated by green dots. An orthogonal step will always be to a cell of a different colour. Diagonal moves cross corners or points and may follow a single connecting edge. In the image on the right possible diagonal moves for the King are shown by a blue dot. A diagonal step will always be to a cell of the same colour. The image on the right also illustrates slides. A slide is a series of steps of the same type (diagonal or orthogonal) made by exiting a cell using the edge or corner that is opposite to the edge or corner by which that cell was entered. Thus the black dots show cells connected by a diagonal slide, while the red dots show a possible orthogonal slide. |
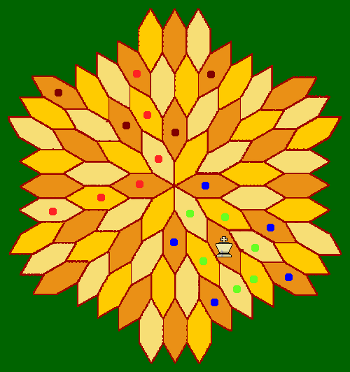
|
| Bishop
|
Slides diagonally. May not
leap over pieces.
The Bishop may move to the cells marked with a blue dot. Note that there is no connection from g1 to j1. Similarly h1-k1 and i1-l1 are not connected. However a1-d1, b1-e1, and c1-f1 are connected. |

|
| Rook
|
Slides
orthogonally. May not leap over pieces.
The Rook may move to the cells marked with a black dot. |
|
| Knight
|
Leaps 2-steps; the first
orthogonally; the second diagonally and continuing away from the
starting cell.
The initial orthogonal steps are marked in light-green for the white knight and in dark-green for the black knight. The move cannot be blocked by pieces occupying these cells reached by the initial step. Possible destination cells reached by the final diagonal step are shown by a white dot.for the white knight and by a black dot for the black knight. |

|
| Queen
|
Moves as either a Bishop or Rook.
|
|
| Pawn
|
May move a single step
orthogonally forward but only if the destination cell is empty (a
passive move).
Possible passive moves are shown by blue dots. For petals a,b,c,d,e,f,h,i,k,l there are at most 3 possible passive moves. For petals g and j there are at most 2. May move a single step diagonally forward but only if the destination cell contains an enemy piece (a capturing move). Possible capturing moves are shown by red dots. For petals a,b,c,d,e,f,h,i,k,l there are at most 2 possible capturing moves. For petals g and j there are at most 3. There is no initial double move. Promotes on reaching the far-most rank - for White.the promotion cells are marked in light-green, for Black in dark-green. |

|
Rules
Apart from the board, initial piece placement, and piece movement (see above) FIDE rules apply.
 This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By Graeme C Neatham.
Web page created: 2009-09-17. Web page last updated: 2020-05-02