CROSS3D CHESS
By Stephane Burkhart (© 2005 Burkhart)
Introduction
"Cross3D Chess" is a 3D chess game where one tries to preserve the same principles as for the traditional 2D game, providing many more opportunities by the additional number of cubes controlled by the pieces on a 8x8x8 board.The opponent pieces are located opposite to each other on table 1 and 8, with a cross pattern having the king as central point (justified by the analysis to follow).
Global displacement is dictated by that of the pawns which move towards the opponent, and by the final objective to trap the opponent king. Rules of promotion, of "prise en passant" from the pawns are maintained, those of castling of the king and the rook too.
The opponent pieces being on a controlled cube can be made captive, the fellow pieces constitute an obstacle.
An analysis of the positions controlled by each piece compared to the 2D ones should allow us to evaluate their required number.
Setup
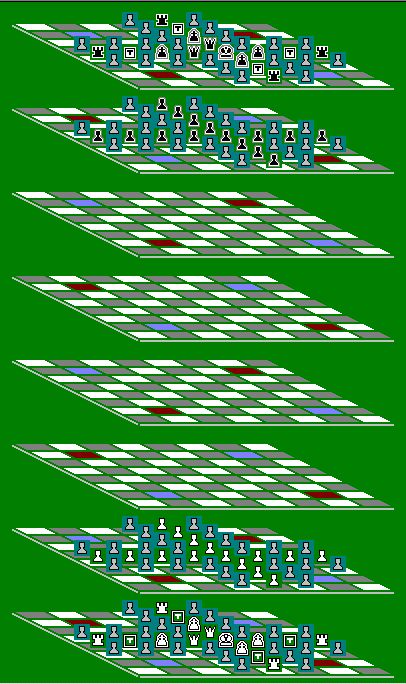
Zillions-of-Games realization with
initial "cross" pattern
Pieces
The Pieces are the usual ones with generalized movement in 3D as described by the rules below.Two sets per color are required with one king and one pawn withdrawn from the game.
The grey pawns are neutral pieces not moving nor capturing, just
there to block side attacks.
Rules
KINGThe king has got a one cube move in each direction: through faces and edges of the cubes. The faces include the outside ones, but also the interior ones constituting the bases of the pyramids having for summit the vertices of the cube (see the rook).
He cannot place himself as a prisoner, i.e. on a position controlled by the opponent.
In 2D, he controls at most 8 squares out of 64, that is to say 12.5% of the squares
In 3D, one counts 26 cubes (27-1) out of 512, that is to say 5.1% of the cubes
The ratio 3D/2D=40.6%
As we keep one king only, he is weakened.
QUEEN
Same displacement as the king but of an unspecified number of cubes or, from another viewpoint, as the rook and bishop joined together. See the Bishop and the Rook for the calculation details.
In 2D, she controls 27 squares out of 64, that is to say 42.2% of the squares
In 3D, she controls 86 cubes (39+21+26) out of 512, that is to say 16.8% of the cubes
The ratio 3D/2D=39.8%
By doubling the number of queens, that is to say two queens present per color, one practically restores the influence found in 2D.
BISHOP
The bishop moves through the edges (in 12 directions in 3D, 4 in 2D)
to remain on his color.
In 2D, one counts 13 squares controlled out of 64, that is to say 20.3% of the squares.
In 3D, 39 cubes (3x13) on 512, that is to say 7.6% of the cubes.
The ratio 3D/2D=37.5%
Again, it is enough to double the number of bishop to have almost 80% of the influence in 2D.
KNIGHT
The knight moves on a sphere of radius 5 (movement 2:1:0 in any direction). It can thus occupy:
In 2D, 8 squares out of 64, that is to say 12.5%.
In 3D, 24 cubes (3x8) on 512, that is to say 4.7%.
The ratio is 3D/2D=37.6%
Same conclusion: one can be satisfied to double the number of knights per color.
ROOK
The rook moves through the facets of the cubes in 6 directions, but also through the base facets of the pyramids made up at the top from the vertices of the cubes, that is to say 8 new directions compared to the traditional rook.

It is noticed that the rook visits in turn the two colors, whatever the type of faces it crosses.
In 2D, it controls at most 14 squares out of 64, that is to say 21.8% of the squares.
In 3D, it grows to 47 cubes (3x7+26) on 512, that is 9.2% of the cubes.
The ratio is 3D/2D=42.2%
Once again, twice more rooks are enough to recover the 2D play.
PAWN
The pawn moves partly like the rook, but towards the opponent board only and one cube at a time (except at the beginning where a two cubes move is allowed) without possible catch, and partly like the bishop one cube at a time towards the opponent board or eventually remaining in the same plan while catching.
This can be understood if one considers that the "side" movement for the pawn in 2D is forbidden because it would correspond to a rook movement in the same plan, whereas nothing can impede an horizontal bishop movement. The pawn can thus defend the side attacks.
In 2D, one hope 3 squares of control out of 64 (including 1 for advancing without taking and 2 for advancing while taking), that is to say 4.7% of the squares.
A 3D, we’ll get 13 cubes (5 to advance like a tower, and 8 to advance while catching like a bishop), that is to say 2.5% of the cubes.
The ratio 3D/2D=53%
Again, two times more pawns reestablish the 2D influence (16 pawns per color).
Finally, catching while passing (bishop catching type) and promotion to the opposite board obey the same rules.
Notes
According to this analysis, 2 sets of crossed pieces (one king and one pawn per color are withdrawn) should be sufficient to maintain the same balance of forces between pieces (in fact, each pair of pieces in 3D but the pawns controls about 3/4 of their 2D correspondant space). There is the assumption that the number compensates the value (two 3D pawns equal one 2D pawn).The king appears weakened, by controlling less positions, and
without direct lateral defense of pawns, but he can castle with 4 rooks
instead of 2, and his movements are more mobile in 3D: one has to
forbid 27 cubes instead of 9 squares !
Nevertheless, some typical CheckMates on the 3 last levels can be achieved:

There exists 2 variants of
the game :

CROSS3D2M variant:
The most interesting and
promising one to me. You must play pairs of pieces (or single if
no pair available) at each turn, without moving twice the same piece,
and you may only capture pairs of opponent pieces (or pass). These
restrictions make it completly different from “Marseillaise” double
game chess.
The motivation is to play twice as much, as you need to move twice the
number of pieces. This renders the Game more playable (around 40 moves)
and less “drawish” (you can checkmate bare King with very few pieces,
as can be appreciated from the Mates already seen earlier).
Finally, it would be possible, though difficult, to play the Game on two boards, one for the
even levels, the other for the odd ones. Levels on which individual
pieces stand would be marked by colored checkers (like coins) under
their base. The "density" of pieces on board would then be the same as
in Orthodox Chess.