sFhIoDgEi
One subset of my variants comprises the "Nested" family: large variants which both players can theoretically ignore half the pieces and half the squares play as some smaller pre-existing variant until one decides, or is forced by what in the smaller variant would be Checkmate, to bring the remainder into play. So far these include Nested Chess, Nested Shogi, Nested Xiang Qi, and Doubly Nested Chess. What is new here is that the two players have a choice of which familiar smaller variant to play - although, just as with the rest, they have the choice of mixing and matching.Although, as its name suggests, this variant combines disguised FIDE and Shogi arrays, inspiration came from the Xiang Qi board. The majority opinion still seems to be that the idea of Chess travelled from India (in the form of Chaturanga) to China (in the form of Xiang Qi) rather than vice versa. Following that assumpion, I wondered whether the board for the latter might have resulted from taking a Chaturanga board in two halves, with one midline thus repeated, and using the corners of Chaturanga squares rather than the squares themselves. Wondering what playing on both interpretations of the board at once would be like, I concluded that having to cope with no original squares in the middle of the River made for too complex a board. It then dawned on me that if combining 9x10 with 8x8 was too awkward, combining Shogi's 9x9 with 8x8 would be more straightforward. Thus what I ultimately used was the actual squares and corners of squares - and mid-edges as well to accommodate pieces holding the entire thing together - of an 8x8 board as a single object without the duplicate midline. I also decided to use modern, rather than ancient, Occidental pieces.
Viewing the whole as a 17x17 board, the Shogi set become oddbound pieces - bound to the intersection of odd ranks and odd files - and the FIDE set become evenbound pieces - bound to the intersection of even ranks and even files. On the odd-even intersections (in both orders) I mostly put unbound pieces, particularly either combinations or enhancements of what would be FIDE pieces on the larger board. Others I explain as I cover them.
Setup
Pieces
The following bound pieces leap two steps, whether or not the halfway square is occupied. Names are explained in Man and Beast 06: The Heavy Brigade, or in the two part-symmetric cases Man and Beast 11: Long-Nosed Generals. | The ALIBABA leaps in any radial direction. Each player has one oddbound and one evenbound Alibaba. A player whose Alibaba of either binding is captured may not move other pieces with the same binding or a subset thereof. The Alibaba is the transformation of the FIDE and Shogi King (see below). |
 | The GOLDTHIEF leaps in the four orthogonal and two forward diagonal directions. Each player has two Goldthieves, both oddbound. The Goldthief is the transformation of the Shogi Goldgeneral. |
 | The SILVERTHIEF leaps in the four diagonal and one forward orthogonal directions. Each player has two Silverthieves, both oddbound. The Silverthief is the transformation of the Shogi Silvergeneral. It is promotable to a Goldthief. |
 | The DABCHICK leaps only orthogonally forward. Each player has nine Dabchicks, all oddbound. The Dabchick is the transformation of the Shogi Point. It is promotable to a Goldthief. |
 | The TUSK leaps only diagonally forward. Each player has five Tusks, all bound to even ranks but odd files. I include it as fitting in well with the other forward-only pieces of the front two ranks. |
 | The VANGUARD leaps as a Dabchick for noncapturing moves but as a Tusk for capturing moves. Each player has eight Vanguards, all evenbound. The Vanguard is the transformation of the FIDE Pawn. It is promotable to an Alibarider, Dabbarider, Elephrider, or Charolais (see all below). |
 | The ALIBARIDER moves in any radial direction. Each player has just one evenbound Alibarider. The Alibarider is the transformation of the FIDE Queen (see below). |
 | The DABBARIDER moves only orthogonally. Each player has one oddbound and two evenbound Dabbariders. The Dabbarider is the transformation of the FIDE and Shogi Rook. It is promotable to a SABOTEUR, the transformation of the Shogi Chatelaine (see below), by the addition of the diagonal component of the Alibaba move. |
 | The ELEPHRIDER moves only diagonally. Each player has one oddbound and two evenbound Elephriders. The Elephrider is the transformation of the FIDE and Shogi Bishop. It is promotable to a HOWDAH, the transformation of the Shogi Primate (see below), by the addition of the orthogonal component of the Alibaba move. |
| [pc _JG_1D] | The DABCHRIDER moves only orthogonally forward. Each player has two Dabchriders, both oddbound. The Dabchrider is the transformation of the Shogi Wing. It is promotable to a Goldthief. |
 | The CHAROLAIS makes any 4:2 leap. Each player has two Charolais, both evenbound. The Charolais is the transformation of the FIDE Knight. |
 | The CALF makes only the two forwardmost 4:2 leaps. Each player has two Calves, both oddbound. The Calf is the transformation of the Shogi Helm. It is promotable to a Goldthief. |
 | The KING moves one step in any radial direction and must be kept out of Check. Each player has one King. |
 | The QUEEN moves any distance through empty intermediate squares in any radial direction. Each player has two Queens. |
 | The MARSHAL moves any distance through empty intermediate squares in any orthogonal direction, like a Rook, or makes any 2:1 leap, like a Knight. Its Knight moves cannot be blocked. Each player has two Marshals. |
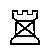 | The CHATELAINE moves any distance through empty intermediate squares in any orthogonal direction, like a Rook, or one step in any diagonal direction, like a Ferz. Each player has two Chatelaines. |
 | The CARDINAL moves any distance through empty intermediate squares in any diagonal direction, like a Bishop, or makes any 2:1 leap, like a Knight. Its Knight moves cannot be blocked. Each player has two Cardinals. |
 | The PRIMATE moves any distance through empty intermediate squares in any diagonal direction, like a Bishop, or one step in any orthogonal direction, like a Wazir. Each player has two Primates. |
 | The DOUBLE RHINO makes alternate orthogonal and diagonal steps through empty intermediate squares, turning 45° alternately left and right between steps. Each player has two Rhinos. I include it as a particularly strong long-range piece for so large a board. |
 | The ROSE makes up to 6 successive Knight leaps between empty intermediate landing squares in one move, differing from the Nightrider by making a turn between each leap, either always left or always right within a move, and alternating between 37° and 53°. Each player has two Roses. I include it as an extended Knight but not extended exorbitantly far. |
 | The FROG moves one step diagonally, like a Ferz, or three orthogonally. Each player has two Frogs. I include it simply because I have been alternating Roses and Frogs in my university+river family of variants and thought it about time to bring them together. |
Rules
A Vanguard on its player's 4th rank (their rearmost possible one) may optionally make a noncapturing move four steps forward. The halfway square must be empty but other intermediate squares may be empty or occupied. They can however be immediately captured En Passant by enemy Vanguards as if they had leaped the usual two steps. This is the transformation of the FIDE Pawn double-step move.An Alibaba and Dabbarider, both evenbound and unmoved, can Castle as long as even squares between them are empty, the Alibaba moving four steps sideways and the Dabbarider to the Alibaba's halfway square. If however the other player replies by immediately capturing the Dabbarider with an evenbound piece, or moving such a piece to the Alibaba's starting square, the Alibaba is captured En Passant. This is the transformation of FIDE Castling.
The King and either Chatelaine, both unmoved, can Castle as long as all intermediate squares are empty, the King moving to the Primate starting square and Chatelaine to the Elephrider one. No part of the King's path may be threatened by an enemy at the time.
A Vanguard reaching its player's 16th rank can go no further unpromoted and so must be promoted to an Alibarider, Dabbarider, Elephrider, or Charolais. This is the transformation of FIDE Pawn promotion.
A Dabchick, Dabchrider, Calf, or Silverthief moving to, from, or within its player's 13th rank or beyond can be promoted to a Goldthief. For the Silverthief this is always optional. For the rest promotion is compulsory on reaching the 17th rank, and for the Calf the 15th as well. This is the transformation of Shogi promotion to Goldgeneral.
A Dabbarider or Elephrider moving to, from, or within its player's 13th, 15th, or 17th rank can optionally acquire all remaining Alibaba moves. This is the transformation of Shogi linepiece promotion. Note that evenbound Dabbariders and Elephriders, including those resulting from Vanguard promotion, never reach these ranks and so can never be promoted.
A player capturing any enemy piece on the intersection of odd ranks and odd files puts it into their Reserve and can, in place of a subsequent move, return it to the intersection of odd ranks and odd files as part of their own army in unpromoted form. This is the transformation of Shogi reintroduction. A piece captured anywhere else goes into a third, neutral Reserve.
A Tusk reaching the 16th rank must be swapped with a symmetric piece from any of the three Reserves.
A player whose oddbound Alibaba is captured cannot move any other oddbound piece. A player whose evenbound Alibaba is captured cannot move any other evenbound piece. This is the transforkmation of FIDE and Shogi Checkmate. An unbound piece reaching the even-file squares of its player's 16th rank can be replaced with a missing evenbound Alibaba to restore such movement, or one reaching the odd-file squares of its player's 17th rank with a missing oddbound Alibaba, to restore such movement. The unbound piece however then goes into the enemy Reserve.
Check, Checkmate, and Stalemate apply to the real King as usual. This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By Charles Gilman.
Web page created: 2007-07-21. Web page last updated: 2016-04-15