Hexagonal Chess
Several different chess variants, to be played on a board, not composed of squares, but of hexes have been designed. One of the most well known of these is Glinski's hexagonal chess. Dave McCooey and a friend developed another hexagonal chess variation in 1978-79. Dave writes:
A friend and I developed a hex-chess variation in 1978-79. Our goal was to create the closest hexagonal equivalent to the real game of chess as possible. I have since seen a few other hex-chess variants, including some that predate ours (e.g. Glinski's), but none are as "equivalent" to real chess as ours is. I realize this is a subjective judgement, but I'll explain my reasons below.
Below, you find Dave McCooey's description of his game.
See also:
- Sample games. Several games that were played by McCooey and others.
- Review.
- ZRF-file for several hexagonal chess variants. File to play this game with the Zillions of Games program.
- Endgame analysis statistics for Hexagonal chess, by Dave McCooey.
Rules
The game is played on a 91-hex board (6 hexes on a side) with the starting position as shown:

The board is colored using three colors. The choice of colours varies, but it is best if one is white. (In all of the boards I have made, the center hex is white.) As the above diagram shows, there are 31 hexes of the center hex's color, and there are only 30 hexes of each of the other two colours. (I perceived white as the most odd-ball of the three colours, and that is why the center hex is white.)
The pieces move according to the following diagrams:
King
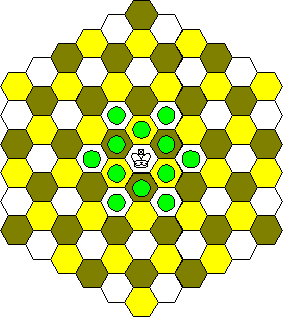
Rook

Bishop
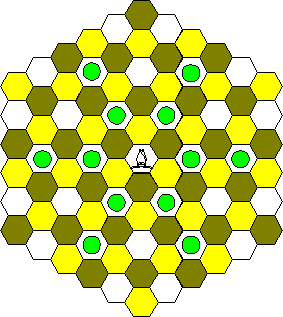
Queen
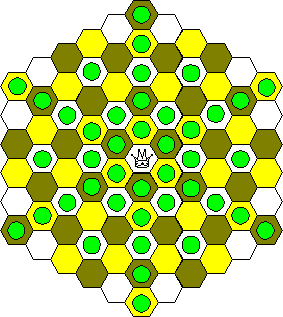
Knight:

Pawn

As in orthodox chess, pawns move without taking straight forward and take diagonally forward (see figure above.)
All pawns, except the center pawn, may move 2 hexes (straight forward) on their first move. The center pawn is excluded in order to prevent White from being able to grab the center hex on the first turn. Of course, White can still get the center hex if he really wants it (in 2 moves), but then, at least, Black has made 1 move of development, which should equalise things somewhat. This rule about the center pawn is the only "arbitrary" rule that has no equivalent in real chess, but at least the rule stems from a desire to equalise the two sides. If the rule proves too "special" or unnecessary, then I have no problem with removing it.
En-passant is also possible using the same logic as in real chess: If a pawn makes a 2-hex move that crosses the attack square of an opposing pawn, then that opposing pawn may capture the pawn by moving to the attacked square that was crossed. Such a capture may only be made on the immediately-following move.
Pawns promote upon reaching any of the 11 hexes on the opponent's side of the board. A pawn may promote to a queen, rook, bishop, or knight, regardless of the number of such pieces still on the board. There is no castling rule.
Checkmate and stalemate are defined as in real chess, and the same outcomes apply: Checkmate is 1-0, and stalemate is 1/2-1/2.
The "diagonal" move, which can be made by the bishop, queen, and king, and by the pawn when capturing, requires further clarification: Such a move is never blocked by occupied hexes that are not on the diagonal itself. The only thing that blocks a diagonal move is an occupied hex that is on the diagonal itself and between the piece and its destination. Thus, a one-step move along a diagonal can never be blocked. For example, the pawn's capture and the king's diagonal move are never blocked.
A knight's move may never be blocked. It "jumps" from hex to hex as in real chess.
Remarks
I have read about the rules to Glinski's version, and realize that my version is identical to his except for three things: (1) the pawn capture, (2) the starting setup, and (3) the stalemate rule. I had no knowledge of his version (or anybody's for that matter) when I developed mine, so the fact that virtually identical versions arose independently supports the idea that they are pretty close to the best hexagonal equivalent of real chess. What I do not understand, however, is why Glinski made his pawns capture "straight" (i.e. like a rook instead of a bishop). All I can think of is that this "straight" capture appeared diagonal to him on the board. It couldn't be that the true diagonal capture is unworkable, because my version has had no problem with it. As for the starting setup, not much can be said except for the minor fact that mine has no unoccupied spaces behind the pawns, as his does. Also, the space between the two forces allowed by my setup (33 hexes total) is closer to real chess (32 squares total) than Glinski's setup (29 hexes total). In particular, Glinski's center seems much too close together.
The stalemate rule used in Glinski's version (outcome 3/4-1/4) is a novel idea that some people have suggested using in real chess. I chose the 1/2-1/2 outcome for my game simply to emulate real chess.
There is one peculiarity we have noticed about my setup: The center pawn begins the game unprotected. Moreover, if a knight lands on that hex, it's checkmate and a triple fork, all in one! Fortunately, this situation exists only at the start of the game and is remedied quite easily. The pawn can either be protected, or, better yet, the pawn can simply be advanced one hex, thus guarding the last free hexes from which a knight can attack the vulnerable hex.
Two advantages of Glinski's and my setup over other variations are (1) side-to-side symmetry, and (2) all pawns are the same distance from promotion. In my setup, the pawns are all seven hexes from promotion, just like in real chess.
I have also created some endgame databases for my variant using retrograde analysis. Currently, I have only done 2-piece endgames with no pawns. Since Glinski's board is the same as mine, and since our pieces (not pawns) move the same, the results are valid for his version as well. Glinski's 3/4-1/4 stalemate outcome should not affect the win-loss ratio in the analysis, but it will subdivide the draw results into a new category halfway between win and draw. For example, my analysis shows that king, knight & bishop draw against a lone king, but, using Glinski's stalemate rule, it might possibly be a forced 3/4-1/4 result.
My endgame databases also include using any of the common variant pieces (chancellor=R+N, pegasus=B+N, and amazon=Q+N), just in case somebody develops a hex-chess variant using these pieces on the same 91-hex board. Here are the more interesting results:
The K+NN vs K endgame is fun to play and exceedingly difficult. I am a USCF-rated expert, and I have not been able to win it yet. For comparison, I would say it is considerably harder than the K+Q vs K+R endgame in real chess. The K+R vs K+N endgame in hex-chess is also very hard.
Dave McCooey Email: dmccooey at mac dot com
Equipment

This game uses two full Chess sets (minus one Pawn of each color) and an extra Bishop for each side. To create your own hexagonal board like the one shown in the photo, see Fergus Duniho's Make Your Own 91-Space Hexagonal Board page.
Link
You can play this game with help of the Zillions of Games program, and this file.Written by Dave McCooey. Webpage made by Hans Bodlaender.
WWW page created in 1995 or 1996. Last modified: September 5, 2001.
