Feeble Los Alamos Chess
In April 2002, Ralph Betza invented Feeble Chess. His idea was to make a variant that would utilize pieces that were as weak as possible, but that would still retain its chess-like play. This turned out to be Weakest Chess, with Feeble Chess a more elegant variant that uses somewhat stronger pieces.My first thought upon seeing this variant was that a playing a game would take many more moves, and require much more patience than orthodox chess. The players would have to see many moves ahead to calculate their attacks or arrange their defenses.
So I decided that Ralph's idea might work better on a smaller board. Also it might be easier for those of us who lack patience. I chose Los Alamos Chess as the small variant to 'Feeblize'.
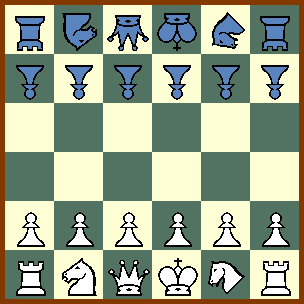 White: Feeble Rook a1, f1; Feeble Knight b1, e1; Feeble Queen c1; Feeble King d1;
Pawns a2, b2, c2, d2, e2, f2.
White: Feeble Rook a1, f1; Feeble Knight b1, e1; Feeble Queen c1; Feeble King d1;
Pawns a2, b2, c2, d2, e2, f2.
Black: Feeble Rook a6, f6; Feeble Knight b6, e6; Feeble Queen c6; Feeble King d6;
Pawns a6, b6, c6, d6, e6, f6.
In the diagram above, the pieces (generally) move one square in the direction they are 'pointing' (ie. the direction in which they are oriented). The exceptions are:
Knights move in their oriented direction one square, then move one square at a 45 degree angle (clockwise) from their current orientation (counter-clockwise for Black). Knights still may leap over other pieces.
Queens move either one square in the direction they are oriented in, or one square at a 45 degree angle (clockwise) from their current orientation (counter-clockwise for Black).
Pawns move simply as orthodox pawns, except they lack the initial two-square move.
A piece may move by simply reorienting itself. Generally pieces may rotate 45 degrees (either way) from their current orientation while retaining their current position. Exceptions to this are:
Queens may rotate 45 degrees or 90 degrees.
Rooks rotate 90 degrees and may not rotate 45 degrees.
Pawns may not rotate.
Otherwise, the rules are as in Feeble Chess.
Notes
While this game does have some of the character of chess, it is missing at least one characteristic of orthodox chess:Pinned pieces. Since there are no 'ranged' pieces, it is not possible to block check, and therefore, there is no concept of pinned pieces. Also the concept of 'forking' is considerably reduced (the Queen is the only piece that can fork).
On the other hand, this variant has a new characteristic -- chasing down. A piece can actually chase another piece, catch up to it, and capture it. A Feeble King can chase down a Feeble Rook or another Feeble King, but not a Feeble Queen.
Another difference is the importance of being able to retreat. In this game, much consideration must be given to being able to retreat when one has attacked into enemy territory. It usually takes several moves to retreat, but usually fewer moves for your opponent to attack the retreating piece.
Written by David Howe.
WWW page created: July 4, 2002.
