Tetrahedral Shogi and Tetrahedral Hexgi
This variant uses a board like Mark Thompson's Tetrahedral Chess but enlarged to side 9 as 2d Shogi's is. This may sound excessive for a 3d board, but a tetrahedron has far fewer cells than a cube of same side length - 165 as against 729 in this case. As I term the extra dimension up and down, I envisage ranks laid vertically, perpendicular to the players' view of each other, and propping up the Black back rank to be level with the middle cell of the White one. This makes the twelve orthogonals forward-right-up, forward-right-down, forward-left-up, forward-left-down, straight right, straight left, straight up, straight down, backward-right-up, backward-right-down, backward-left-up, and backward-left-down.Unlike Mr. Thompson I make use of the Bishop's diagonal, as this geometry preserves especially well the 2d differences between that direction and the Rook's orthogonal. The six such directions are straight forward, right-up, right-down, left-up, left-down, and straight back. An oddity is that Bishops are bound to 1 in 4 cells, and specifically to odd or even ranks, rather than to the alternate ones of square and cubic geometry, but that makes Shogi Bishops' ability to return on new bindings all the more pertinent. As the board just exceeds twice the Shogi one's cells I double army size (except for Kings and one Point aside) to give two Bishops, one on each even-rank binding, aside. One especially Shogi-friendly feature of this geometry is that Gold directions exceed Silver ones - 13 and 10 respectively. This is the exact reverse of the - therefore less Shogi-friendly - cubic geometry.
A Thompson precedent that I do follow is accepting that Knight moves are a little too long on this board, and substituting the move used by Siegmund Wellisch in his 2d hex game. As mention of Wellisch hints, this board contains hex as well as square-cell planes - its faces are triangles of hex cells. As in my 2d Shogi-Wellisch hybrid Hexgi, I use only the most forward moves of Wellisch's piece. Mark Thompson himself speculated about a Shogi-style variant with selected-orthogonal pieces, but as far as I can see never went ahead with one. This made me wonder whether I could use this board for a 3d Hexgi, with an extra pair of piece types for the extra pair of directions. I added one as a subvariant.
Two ideas that I rejected were a Tetrahedral Mitregi and a Tetrahedral Altorth. The great feature of the Mitre and Cross in Mitregi (and in my cubic variant Tunnelshogi) is that they have multiple forward diagonals in contrast to the single forward orthogonal. On a tetrahedron it is root-2 diagonals that have but one forward direction, which from many cells runs out before the promotion zone. Altorth is specific to the Glinski/McCooey orientation, which again has a straight forward orthogonal not replicated on a board with camps at opposite edges of a tetrahedron.
Setup
Throughout these diagrams I depict each rank as a square-cell board, with the Black back rank along the top and the White along one side. Successive ranks on each side converge on a square middle rank depicted in one corner. Although the original Tetrahedral Chess does not use Bishops its page depicts their bindings as four colours. Here is the balance of bindings on the side-9 board:
This is the Tetrahedral Shogi array. Notice how Rook and Bishop starting cells combine emulating 2d Shogi with having Bishops on both bindings. With only 9 cells on the first rank Silvers are brought forward to the near-empty second, and Saltires to the third to fill gaps between only 17 Points on 21 cells. This places them only two leaps from optional, and three from compulsory, promotion - one fewer than the Helms of 2d Shogi.
Tetrahedral Hexgi replaces the King/Prince move and its subsets with the General/Wazir move and subsets of that. These include two each of four rotations of a basic type. In place of Bishops are further (and unpromotable) Rooks.
Pieces
Pieces common to both variants: | The ROOK (Hisha=Flying Chariot) moves any distance through empty intermediate cells along any of the twelve orthogonals listed in Tetrahedral Chess. It is promotable in Tetrahedral Shogi to a CHATELAINE (Ryuo=Dragon King), which can also move one step as a Bishop, but unpromotable in Tetrahedral Hexgi. |
  | The WING (Kyoosha=Fragrant Chariot) moves any distance through empty intermediate cells, and the POINT (Fuhyo=Foot Soldier) one step, orthogonally forward. Though a single direction in square-board Shogi this expands to 2 directions in 2d hex Shogi and up to 4 here. Both are promotable to Goldgeneral in Tetrahedral Shogi and to Wazirranker in Tetrahedral Hexgi. My piece article Man and Beast 01: Constitutional Characters explains the names - but see notes. |
 | The SALTIRE has a move with two stages: one step (but therefore two ranks) along the straight forward diagonal followed by one step along any same-rank orthogonal. It cannot be blocked. Note that this move is the same as the forward hex diagonal of either a face of the board or a plane parallel to one. As Helm analogue it is promotable to Goldgeneral in Tetrahedral Shogi and to Wazirranker in Tetrahedral Hexgi. Man and Beast 01 again explains the name - but see notes. |
 | The KING (Japanese name varies between armies) can move one cell in any orthogonal and diagonal direction. It must be kept out of check. It is not promotable. |
 | The BISHOP (Kakugyo=Angle Mover) moves any distance through empty intermediate squares on the diagonals of any square plane - the obvious ones within ranks, and straight forward and backward in two-rank steps. It is promotable to a PRIMATE (Ryuma=Dragon Horse), which can also move one step as a Rook. |
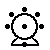 | The GOLDGENERAL (Kinsho) moves one step either as a Rook or along the straight forward diagonal. It is not promotable. |
 | The SILVERGENERAL (Ginsho) moves one step either as a Bishop or along any forward orthogonal. It is promotable to Goldgeneral. |
 | The GENERAL moves one step along any orthogonal, like a Wazir, but unlike the latter piece and like the King it must be kept out of check. It is not promotable. |
 | The WAZIRRANKER moves one step along any of the eight rank-changing orthogonals - a Point that can go backward as well as forward. This piece is rankswitching, that is, it always moves from an odd to an even rank or vice versa and so cannot lose the move. My page article Man and Beast 12: Alternative Fronts explains the name. In this variant it is a promotee only. |
  | The DEXTER moves one step along the player's five right orthogonals and their straight left one. The SINISTER moves one step along the player's five left orthogonals and their straight right one. As they mirror each other each can become the other at the end of a promotion-zone move. They can do so any number of times. The pieces are the Hexgi ones extrapolated to this particular 3d board. The names are Latin for right and left, and the heraldic terms for those sides of a shield from the carrier's viewpoint (and the opposite from the opponent's). |
  | The CHIEF moves one step along the five upward orthogonals and the straight downward one. The BASE moves one step along the five downward orthogonals and the straight upward one. As they mirror each other each can become the other at the end of a promotion-zone move. They can do so any number of times. The pieces are further extrapolations of the Dexter and Sinister above. The names are the heraldic terms for the upper and lower parts of a shield. |
FRU - Wing (any distance), Silver, Point, Dexter, Chief
FRD - Wing (any distance), Silver, Point, Dexter, Base
FLU - Wing (any distance), Silver, Point, Sinister, Chief
FLD - Wing (any distance), Silver, Point, Sinister, Base
straight right - Dexter, Sinister
straight left - Dexter, Sinister
straight up - Chief, Base
straight down - Chief, Base
BRU - Dexter, Chief
BRD - Dexter, Base
BLU - Sinister, Chief
BLD - Sinister, Base
Summary of pieces that can use each 2d diagonal:
straight forward - Bishop (any distance), King, Gold, Silver
other five - Bishop (any distance), King, Silver
Rules
There is no intital double-step move, En Passant, or Castling.A player capturing the other's piece puts it into a Reserve, and can reintroduce it at any time. Dexters and Sinisters can return in either form, likewise Chiefs and Bases, but the rest must return unpromoted and able to move in that form. Reintroducing a forward-only piece on the King cell gives it a far greater spread of destinations than it had on its array cell.
As in Shogi a player's promotion zone comprises the far edge plus cells one or two orthogonal steps short thereof, coinciding with the three ranks of the enemy camp. A promotable piece starting or ending a move on such a cell may be promoted at the end of that move. Promotion is optional unless the piece has no further move unpromoted.
Check, Checkmate, and Stalemate are as in FIDE Chess.
Notes
In Tetrahedral Shogi, pieces can be represented as themselves with just the substitution of Helms representing Saltires. In Tetrahedral Hexgi it makes more sense to represent the unpromotable Rooks with Goldgenerals, use physical Rook and Bishop pieces indiscrimately unpromoted to represent the Base and promoted to represent the Chief, and use Silvergenerals likewise for the Sinister and Dexter.This geometry reinforces my use of the same names for pieces using the cubic and the hex root-3 diagonals, as a single type of direction fits definitions of both. Symmetric pieces - the short-range Viceroy and long-range Unicorn - are bound to a third of a hex board, a quarter of a cubic board, and still less of a hex-prism one, but are paradoxically unbound on a xyrixa one. This makes them better Knight analogues on such a board than in 2d hex variants such as Wellisch and Altorth. The forward-only piece names Point, Cross, and Saltire are named for their move patterns as viewed on a face-to-face cubic board. On this page's board the Point makes a saltire pattern, the Cross a point pattern, and the Saltire a cross pattern. This is a pity but as cubic is, rightly or wrongly, the commoner 3d geometry I have let the cubic names stand.
The Unicorn's unbound character also makes this geometry especially suited to a variant on a Scottish theme. It occurred to me that the severe binding of the Bishop would make this very variant's board suited to one based on sectarianism in that state. Back ranks could run Rook, Unicorn, enhanced Bishop, Queen, King, Duchess, enhanced Bishop, Unicorn, Rook. The enhanced Bishops - a choice of Cardinal (Bishop+Knight, for Catholics), Moderator (Bishop+Viceroy, for Prebyterians), Primate (Bishop+Wazir, for Episcopalians) - could have to differ between the players. Thus here is how the Black back rank will look with each army:
The second rank might contain a mixture of oblique leapers, including in places to block compound pieces from getting out to quickly. The third could either be filled with Points or have a mixture of 16 Points around the edge with 5 Saltires in the middle. In the latter case Points would have be advanced before Saltires in order to protect them. I would be interested to know whether anyone thinks this idea worth developing into a subvariant on this page.
This is my first use in a game of Chief and Base in the sense of upward- and downward-orientated pieces, as defined in Man and Beast 12. I did however foresee this usage sufficiently to substitute the name Foundation in Gutenschach for a planar pieces which Gavin Smith invented under the name Base.
There can be tetrahedra of any side length upwards of 5. One of side 8 could have a "normal" back rank (substituting Viceroys for Knights again) and 14 Pawns. As however its 120 cells are nearly the 121 of my Nearlydouble Chess a more interesting pattern might be RRBQKBRR on the back rank, two lots of -V-B-V- on the next (giving a Bishop aside on each binding), and 2 gaps in a 3x6 Pawn rank. A tetrahedron of side 12 would have 364 cells - one for nearly every day of the year and in particular one for each individual gift in The Twelve Days of Christmas. Hopefully most of you can see the mathematics behind this fact. This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By Charles Gilman.
Web page created: 2009-06-13. Web page last updated: 2016-07-08
