
Check out Grant Acedrex, our featured variant for April, 2024.
Check out Grant Acedrex, our featured variant for April, 2024.

Stefanos Pantazis, editor of The US Problem Bulletin, has sent me two problems that appeared in that journal and did win a prize there.
This is the solution of the second problem: You can also look at the first problem: a series selfmate in 17 moves.
This problem was composed by Michel Caillaud, was published in The US Problem Bulletin in 1994, and won a First Prize.
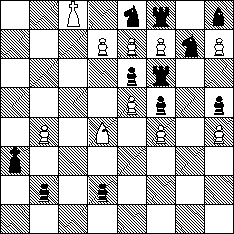 White:
White:
King c8; Bishop d4; Pawn b4, d7, e5, e7, f4, f7, h4, h7.
Black:
King a3; Rook f6, f8; Knight e8, g7; Bishop h8; Pawn b2, d2, e6, f5, h5.
Circe. h=4: Helpstalemate in four moves.
(b) Move the black king from a3 to a4, and solve the problem again.
= means promotion, e.g. 1.b1=B means that a black pawn promotes to a bishop; + means a check; rebirths are written between brackets, e.g., (Ng8) denotes a knight being reborn on g8. Turns are denoted as first the move of black, and then the move of white.