Ravioli Chess
By Antoine Fourrière
Introduction
Ravioli Chess borrows its main idea from Chessma: using "meta-squares". (Meta-squares were also used by Joao Pedro Neto in The Central Squares and David Howe in Quad-Square Chess). The common characteristic of these games is that they blend a few elemental squares into a square, and to consider that a piece may land/travel/stop there only if it may land/travel/stop on any of the virtual squares which compose it.Ravioli Chess combines two 8x8 Orthochess boards by equating their border squares, like in a ravioli whose two layers of pasta are separated in the middle and squeezed together on the fringes.
When you introduce a different topology or different rules, it seems a nice idea to have some pieces which are specially adapted to your changes. (Think of the Voidrider in Fergus Duniho's Voidrider Chess.)
Board and Setup
Ravioli Chess is played on a 100-square board made of two 8x8 boards, which can be viewed as three parts, the common outer ring and the two remaining 6x6 inner boards. The outer ring fetches the usual light and dark squares, while the inner rings uses these shades within two colors, as Charles Gilman suggested in Grossraumschach
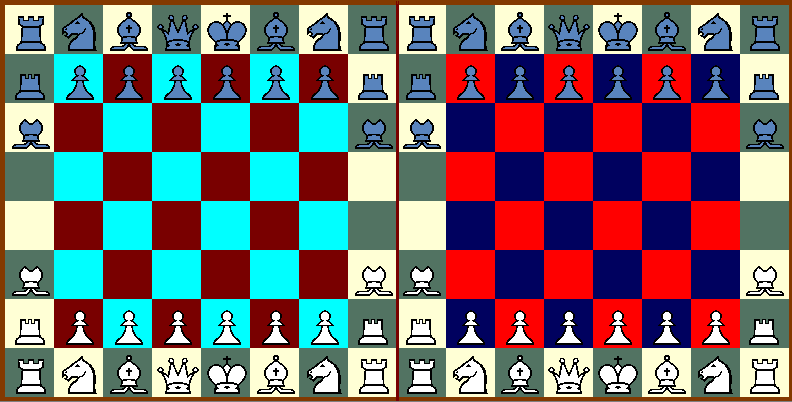
|
|
The Pieces
The King, Queen, Rook, Bishop, Knight and Pawns move as in International Chess, that is, a move is legal if and only if it is legal on at least one 8x8 board. Thus they can never commute directly between the two 6x6 inner boards.The Bishop is still bound to light squares or dark squares, the Knight still commutes between them.
But there is a couple of special pieces, which are allowed to commute directly between the inner boards.
The Wizard moves as a Halfling Slip Bishop, that is diagonally to the first square, or to the third square, but only if the first square is empty and the fifth square within the board. (See here about Halflings and here about Slip Pieces.)
The Wizard may also commute one square diagonally (but not triagonally) between the two inner boards. Thus it is bound to the red squares or to the blue squares as long as it stays on the inner boards.
The Wazird moves as a Halfling Slip Rook, that is orthogonally to the first square, or to the third square, but only if the first square is empty and the fifth square within the board.
The Wazird may also commute one square orthogonally or triagonally between the two inner boards. Thus it always switches between a red square and a blue square as long as it stays on the inner boards.
Other rules
The game is conducted by the rules of International Chess, except where noted otherwise. Stalemate or perpetual check is a draw.Castling is forbidden if there is an intermediate square under attack on only one 8x8 board.
The play of the game
King + Queen doesn't give mate against a lone King, so it may be wise to sacrifice a lot of material to exchange the last Pawns and prevent the enemy from getting a second Queen (Still, King + 2 Rooks mates.)Variant
- OrthoPawns and BeroPawns features normal Pawns on only one board, and Berolina Pawns on the other. (An advanced Pawn may end up on the "other" inner board.)
Zillions
There is a zrf. To complete a move from the outer ring to an inner board, you must click on the elemental square which is on that board. So the little green dots may be misleading.When I wrote the zrf first, Zillions kept all his officers on the outer ring, to double their value. I had to write dummy boards and dummy pieces, so that Zillions valued each piece with the same (double) standard. Zillions also inflated slightly the value of a Pawn, because of a rewriting of the procedure regarding promotions, so I added bogus points. You can open the zrf and change the relative values of the pieces by adding or substracting some (1000-points)-commands.
Written by Antoine Fourrière.
WWW page created: October 8th, 2003.
