Elevator
Ben Good
Introduction
I originally conceived the idea and wrote the rules for Elevator on June 22 and 23, 1998. At the time, I had almost no experience with 3D Chess. My goal was not to create some kind of perfect conversion of FIDE Chess into a 3D version - I still maintain that such a game does not exist - but to create a fun and playable 3D Chess variant that used the Elevator board. I thought of the board first, and made the rules and pieces to fit the board. I wrote it all out in one sitting, making it up as I went along. The webpage that was made from this effort was basically a rough draft and it read like one.I didn't do anything with the game after that. I didn't playtest it even once, or think about rules changes, or think about constructing a board. To be honest, after creating it, I actually expected the game to be very bad, and so I mostly forgot about it. But in August 2002, L. Lynn Smith sent a me a ZRF for the game, and I was surprised to discover that the game plays quite well. Only one significant rule change was made. The purpose of this updated webpage then is to present the rules in a more polished form, to clarify amibiguities in the original rules, to provide better diagrams, to link to the ZRF, and to discuss the game in a little more depth. These rules generally assume that the reader is familiar with the rules of Chess, although I have provided some additional links throughout.
This webpage would not exist without the efforts of L. Lynn Smith, who in addition to coding the ZRF, also made changes to it when I asked for them, designed the graphics, made a special ZRF for the purpose of making the diagrams for this page, and made suggestions regarding the rules.
The Board
Consider a board, 8x8 in size. It can be divided into 16 groups of 2x2, as shown in the diagram below.
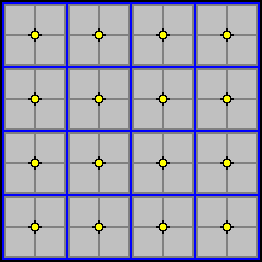
Now suppose that each 2x2 area is extended into the third dimension, creating 2x2x1 blocks. Each of these blocks is called an elevator. Next imagine a vertical support pole running through the center of each elevator, for a total of 16 poles. Each pole has four different heights, or levels, at which an elevator can stop. The levels are numbered one through four, with one being the bottom level and four being the top - think of them as being numbered like the floors of a building. On each pole there are three elevators. Each pole will them have empty space at one of the levels, this empty space is called the elevator shaft. The result as a board that is essentially 8x8x4, but because of the empty shafts, it actually has the same number of playing fields as an 8x8x3 board. This means that the elevator board is exactly three times the size of a standard Chess board.
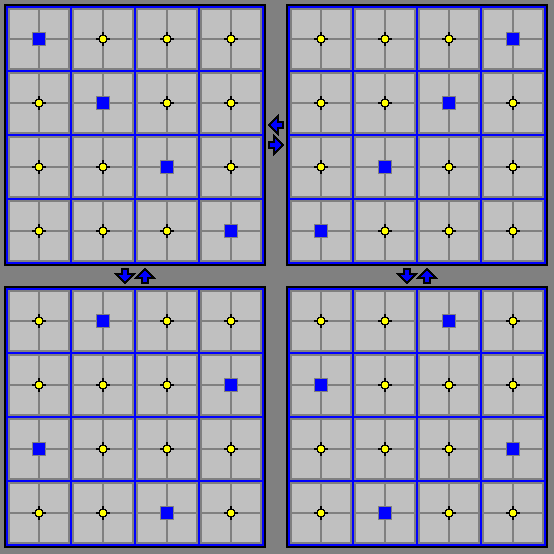
The diagram below shows all four levels as they appear in the Zillions ZRF. The levels are arranged with level one in the lower left, level two in the upper left, level three in the upper right, and level four in the lower right. With this arrangement, all levels are adjacent to the ones to which they would also be adjacent in an actual board. The arrows between the levels give a visual aid to remembering which boards are adjacent.
The yellow circles represent the elevator poles, meaning everywhere you see a yellow circle, there is an elevator there. Where you see only a blue square, there is an empty shaft. Ideally the shafts would be blue throughout the entire section, with only the square outlines remaining, but the current limitations of Zillions coding do not allow for this. It is actually quite easy to get used to the small blue squares.
It is also preferable to checker the squares, since this does in fact make it easier to visualize diagonal moves. Again because of limitations of the Zillions program, checkering the elevators would also require checkering the empty shafts, which we felt was too visually distracting. If a future upgrade of Zillions allows for an improved Elevator ZRF, we will post it as soon as possible.
3D Chess players think of the spaces for each piece as a series of three-dimensional cells, not as simply flat surfaces. So while it is possible to visualize each elevator as a simple 2x2 platform, it will make much more sense to think of them as three-dimensional spaces, such as little boxes or cages. In particular, the rules for the flying pieces will seem much more logical when the elevators are viewed in this manner. In the rules for the pieces below, I refer to the locations on the board as cells instead of squares.
Moving Elevators
Elevators can be moved up and down along the poles. An elevator can only be be moved into empty space not occupied by another elevator, and it can only be moved to an adjacent level. An elevator on the first level can not be moved down, and an elevator on the fourth level can not be moved up. Elevators can not be moved sideways. Pieces can only end their moves on cells occupied by elevators, although some can move through empty shaft space as long as they do not stop there.
On each player's turn he can move a piece or move an elevator. The
movement of the pieces is described in the next section. To move an
elevator, a player must have control of that elevator. Having control
of an elevator means the player:
- has at least once piece on the elevator.
- has more pieces on the elevator than his opponent.
Pieces
Each player starts with 48 pieces. Just as the board is three times the size of a standard Chess board, the players start with three times the number of pieces in a standard Chess game.Unlike many (but not all) 3D Chess games, the pieces do not move the same way in the vertical planes as they do in the horizontal planes. The game is designed so that 6 out of the 9 types of pieces require travel by elevator to change levels. Therefore, when the piece descriptions below discuss piece movement, they are referring to a movement on a single level, unless it is specifically stated otherwise.
In order to save space on the webpage, most of the piece diagrams below only show a portion of the board.
The Pawn
Each player starts with 24 Pawns. Pawns move without capturing one cell forward or one cell sideways. They capture one cell diagonally foward. Pawns can never move or capture in any backwards direction.
Pawns on their second rank can also move two cells directly foward. They can not jump other pieces when moving this way. Pawns can make this double-step even if they have already moved - they may have moved sideways from their starting position, or they may have moved forward and then been pushed back to the second rank by an Ox. This rule allows players to determine if a Pawn can make a double-step just by looking at the board, instead of requiring them to consult with the game record. Pawns that make a double-step from the second rank can be captured en passant by opposing Pawns on the fourth rank. (If you're not familiar with en passant, you can read about it on this page.)
It is possible for Oxen to push Pawns back to the first rank as well. Pawns on the first rank can also make a double-step forward, whether they have moved or not. Pawns that make a double-step from their first rank can be captured en passant by opposing Pawns on the third rank.
Pawns reaching their seventh rank or eighth have the option of promoting. Promotion is to any piece of the player owning the Pawn that has been captured; if no pieces have been captured then promotion is not allowed. Promotion is never required, so it is possible to have an unpromoted Pawn on the eighth rank. If a Pawn does not promote at the end of a move, it can not do so until it moves to another cell on the seventh or eighth rank; it can not promote in place without moving.
Pawns can only change levels by using elevators.
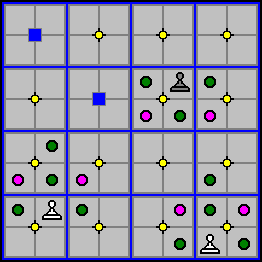
In the diagram below, the Pawns can move without capturing to the cells marked with a green circle, and they can capture any pieces that would be located on a cell marked with a purple circle.
The Walking Knight
Each player starts with 4 Walking Knights. The Walking Knight moves and captures either like a Chess Knight or it makes a single orthogonal step. It can leap over other pieces or elevator shafts. The Knight only changes levels via elevator.
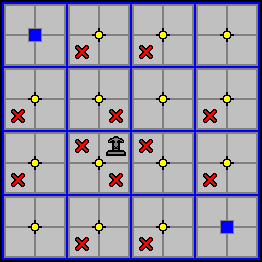
In the diagram below, the Walking Knight can move or capture to any of the cells marked with a red X.

The Walking Camel
Each player starts with four Walking Camels. The Walking Camel moves and captures either like a Camel or it makes a single orthogonal step. The Camel can be thought of as a 'long Knight', it is a (1,3) leaper instead of a (1,2) leaper like the Knight. It can leap over other pieces or elevator shafts. The Camel only changes levels via elevator. Note that because of its single step, the Walking Camel is not colorbound like the standard Camel.
In the diagram below, the Walking Camel can move or capture to any of the cells marked with a red X.
The Vaulting Prince
Each player starts with two Vaulting Princes. The Prince moves and captures one cell in any direction, orthogonally or diagonally. Additionally, the Prince can leap without capturing exactly three cells in any direction, orthogonally or diagonally; when moving this way it can jump over other pieces or elevator shafts. The Prince only changes levels via elevator.
In the diagram below, the Vaulting Prince can move or capture to any of the cells marked with a red circle, or it can move without capturing to any of the cells marked by a green X.
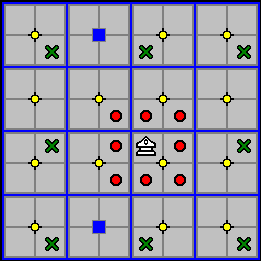
The Ox
Each player starts with four Oxen. The Ox moves without capturing either like a Chess Knight, or it leaps exactly two cells in any direction, orthogonally or diagonally. It can leap over other pieces or elevator shafts when moving this way. The Ox can only capture, however, by moving a single step in any diagonal direction, and it can not move in this way unless it is capturing an enemy piece. The Ox only changes level by elevator.
In the diagram below, the Ox can move without capturing to any cell marked with a green X, or it can capture to any of the cells marked with an orange circle.
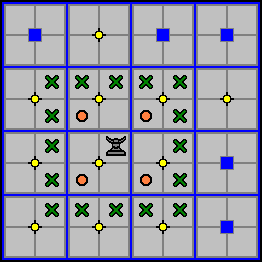
The Ox can also push other pieces. It does so by moving either one or two cells in any orthogonal direction - the pieces it encounters are then pushed with it. Pieces, friendly or enemy, that are pushed off the edge of the board or into elevator shafts plunge to their death and are considered captured. There is no limit to the number of pieces an Ox can push (of course the size of the board actually limits the Ox to pushing seven pieces at once), and it can consolidate an empty cell between pushed pieces. The first piece the Ox pushes, however, must be on an adjacent cells. Also, the Ox can not push other Oxen of either color. Examples are given below.
In the diagram below, the Ox can push pieces by moving to any of the cells marked with a blue circle.
Below is an example of an Ox pushing several other pieces. The diagram on the left shows the Ox and other pieces before the Ox moves. The Ox moves two cells to the right, pushing the entire line of pieces ahead of it. The Black Camel and Black Knight are pushed into the elevator shaft and are captured. The diagram on the right shows the position after the Ox has moved.

Below is an example of an Ox consolidating a group of pieces by pushing. The empty space between the two White pieces does not prevent the Ox from pushing the two Knights. The Ox moves two cells to the right, pushing all four pieces and eliminating the empty space between the pieces. The final position is shown on the right.

Below are two examples of situations where the Ox can not push. On the left, the Ox can not push the Pawns because he is not adjacent to them at the beginning of the move. On the right, none of the Oxen can push any pieces because doing so would involve pushing another Ox.

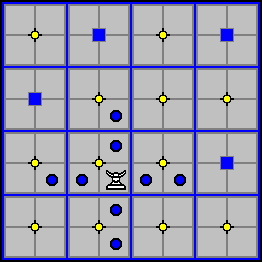
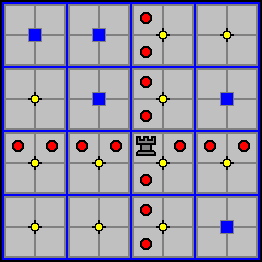
The Flying Rook
Each player starts with four Flying Rooks. Like the Chess Rook, it moves and captures by moving any number of unobstructed cells in any orthogonal direction.
In the diagram below, the Flying Rook can move or capture to any of the cells marked with a red circle.
Like the pieces previously described, the Flying Rook can change levels by riding on an elevator. But in addition to this, it can change levels during the course of its move by using empty elevator shafts. When a Flying Rook is moving and it reaches an empty shaft that is on the same level as the one on which the Rook began its move, it can then move to the corresponding cell on an adjacent level and continue moving in the same direction. The Rook can not leap over shafts and continue on the same level. When the Rook enters a shaft, it must use the first cell it reaches to change levels. The Flying Rook can only make one level change per move - if it changes levels and reaches another shaft, it must stop.
In the diagram below, the Flying Rook can move or capture to any of the cells marked with a red circle.

It is largely because of this rule that I previously suggested thinking of the elevators as three-dimensional objects instead of flat platforms. If one considers the elevators to be flat platforms, this rule may seem illogical and asymmetrical - a Rook moving up a level seems to be doing so even though it's the platform below him that is out of the way, while inevitably there will still be a platform above him where he changes levels. If the elevators are thought of as three-dimensional containers, however, the rule makes a lot of sense. Now the removal of an elevator takes away both floor and ceiling, allowing the Rook to move either way. The floor and ceiling of the elevators can be thought of as having one-way doors in them that only allow pieces to pass through coming from the outside in.
A characteristic of the Flying Rooks (and the other flying pieces as well, see below) is that it is possible for one Rook to be attacking another without that Rook attacking back. The diagram below illustrates this: the White Rook on level two attacks the Black Rook on level three - the red circles mark the path that the White Rook's would take to make the capture - but the Black Rook is not threatening the White Rook.
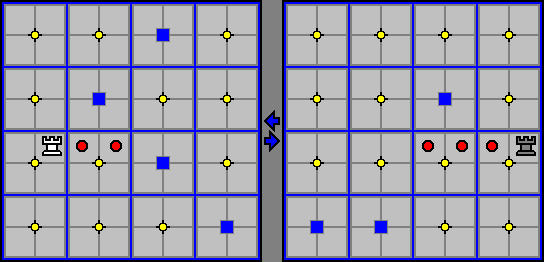
Note that it is possible, however, to construct a sitatuion where two Rooks on different levels simultaneously attack each other.
The Flying Bishop
Each player starts with four Flying Bishops. Like the Chess Bishop, it moves and captures by moving any number of unobstructed cells in any diagonal direction. Unlike his Chess counterpart, however, the Bishop is not colorbound as long as there is at least one Ox left on the board.
In the diagram below, the Flying Bishop can move or capture to any of the cells marked with a red circle.
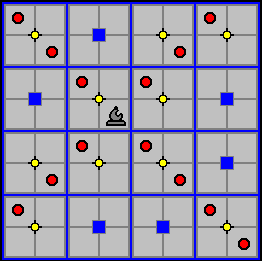
Like the Flying Rook, the Flying Bishop can change levels either by riding on elevators or using the empty shafts. All the rules for level changes that apply to Flying Rooks apply to Flying Bishops as well.
In the diagram below, the Flying Bishop can move or capture to any of the cells marked with a red circle.
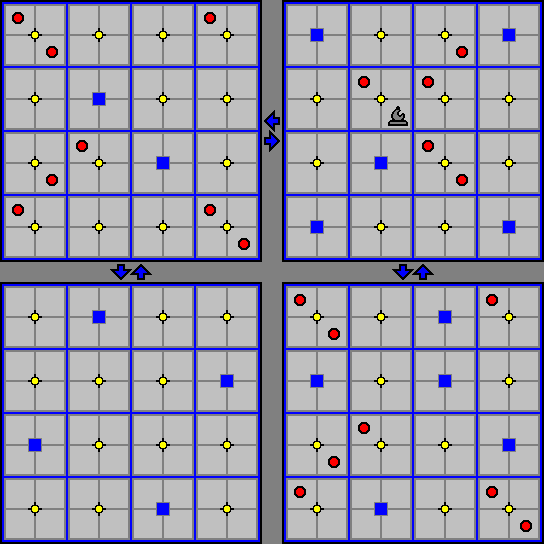
The Flying Queen
Each player starts with one Flying Queen. Just as the Chess Queen has the powers of both the Bishop and Rook, the Flying Queen can move either as a Flying Rook or a Flying Bishop.
The King
Each player starts the game with one King. If he loses his King, he loses the game. The King moves or captures one cell in any direction. He can only change levels by elevator.
In the diagram below, the King can move or capture to any cell marked with a red circle.
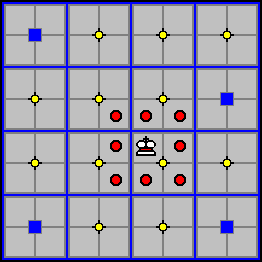
If the King is attacked, he is in check, and the player owning the King must make a move so that the King is out of check at the end of the move. If he has no way out of check, he is checkmated and loses the game. It is legal to remove check by moving the elevator on which the King is standing. Note that if the King is in check from a Flying Bishop, Rook, or Queen, moving the elevator will not get the King out of check.
Setup
The diagram below shows the position of the pieces and elevators at the beginning of the game.
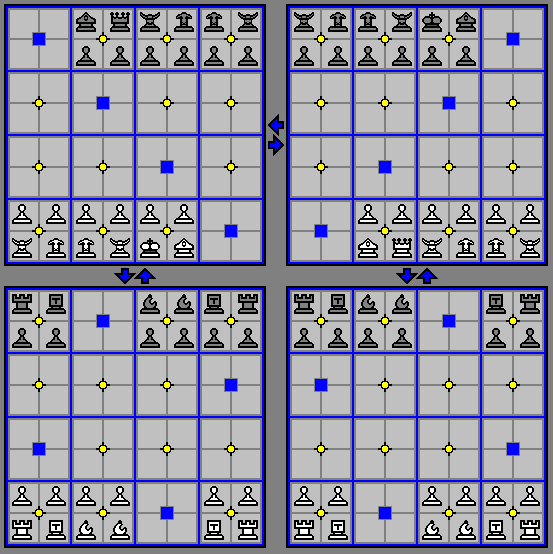
Rules
White moves first.Stalemate is a draw. If neither player has sufficient material to force checkmate it is also a draw. Three-time-repetition, however, is a loss for the player who causes third repetition, in effect forcing him to move somewhere different.
Notation
The ranks and files are the same for each level as they are in Chess, the levels are numbered with one at the bottom and four at the top. Each cell can then be represented by its level number, file letter, and rank number. The White King, for example, starts the game on 2e1. The following abbreviations are used for the pieces:
K - King
Q - Queen
I - Prince
R - Rook
B - Bishop
N - Knight
C - Camel
O - Ox
P - Pawn
The elevators are own their own system of files (a-d) and ranks (1-4). Elevator is abbreviated by E, and U and D are used to designate that the elevator moves up or down respectively. When a player moves an elevator, he notates it by writing the elevator's starting location, and following it with U or D, depending on which way it's moving. So if Black wishes to start off the game by moving the elevator with his King up to level 4, it would be notated as E3c4U.
It is helpful to notate pieces pushed by an Ox, because only showing the Ox's destination cell can be ambiguous. For example, from the starting position, White could play O2a3. But this could mean two different things - either the Ox jumps over the Pawn on a3, or it pushes the Pawn to a4. So O2a3 must be interpreted as meaning that the Ox leaps the Pawn, and if he wants to push it, the player must show the Pawn move in the notation as well with O2a3/Pa4.
Variants
L. Lynn Smith and I discussed quite a variety of variants for this game, but most were rejected as either having inherent problems or being too minor of a change to be significant. The best idea is still the Wonkavator variant, in which elevators can also move sideways on the same level. Such a game would make the still-unsolved problem of construction of a physical board that much more difficult, although certainly Zillions could handle it.Computer Play
If you have Zillions of Games installed on your computer, you can play this game. Download the file here.If you are interested in playing by email, you can email me here.
Equipment
In the original 1998 webpage I started this section off with "Ha. You didn't really think I'd built one did you?", which my friends found amusing. Unfortunately, as of right now I am not any closer to solving the problem of designing an elevator board than I was four years ago, even though I have recently given it some thought. Clear plexiglass with painted dark squares is standard for 3D Chess boards, and creating forty-eight 2x2 sections would not be a problem, except that it may be difficult to get them exactly the same size so that they line up well on each level. Metal poles could be used as the elevator supports, although the board would require a top as well as a base to stabilize the poles. The real problem though is creating a system that would allow the elevators to easily slide from one level to another but also stay in place on the different levels when they are not moving, and getting the elevators to line up exactly on each level. I'm envisioning a setup where to move an elevator, the players need only apply some pressure by hand to push the elevator to the next level and then it clicks into place until it is ready to move again. But I have no idea how to construct something like this. There is the additional problem of reaching in to move elevators on the four inner poles, since both poles and pieces may be getting in the way.Coming up with pieces for the game is problematic as well. If I am going to spend the time, effort, and money to build a board, then I want reasonably attractive pieces to go with it. More conventional solutions such as using different size pieces from different sets will not be sufficient. And as much as I love the Exchess pieces, using them for this game would probably be prohibitively expensive, since two exchess sets and three standard Chess sets would be required. But I don't know of any other commercial variant that contains more than two new types of piece. I may attempt to make my own simplified geometric wood pieces, such as those used in Hans Boedlander's Gala set.
Peter Aronson has pointed out a more practical way to play this game, which is simply to use a 4x8x8 board with no moving parts. Colored tape can be used to mark the 2x2 grid on each level, and a 2x2 square of cardboard can be placed over the squares for each shaft. When a player "moves an elevator", he moves the pieces by hand to their new location, then transfers the shaft marker to the vacated spot. Players can also put some kind of piece in the center of elevators marking it as such, although this would not be necessary. (This idea is actually the basis for the ZRF as well. Zillions generally goes not support moving squares, so Smith got around this by making the elevator a piece (the yellow pins) that pulls the elevator's pieces along with it when it moves. The blue squares of the shafts are drawn in as part of the board, and the pins cover them up where there is an elevator.)
Additional Remarks
Since the board is exactly three times the size of the standard Chess board, and the number of starting pieces is exactly three times as many as in standard Chess, it is reasonable to expect that an elevator game will take three times as long to play as a standard Chess game. Indeed I have generally found this to be true.The only significant change from the original game is the rule allowing a King to move out of check by moving an elevator. The original game did not allow this, but L. Lynn Smith convinced me that it was not needed, and it was problematic for Zillions to enforce. The new rule also helps justify the movement of the flying pieces, since moving an elevator will not remove check from a flying piece.
The Ox is a slightly modified version of the piece of the same name in Jim Aiken's not-quite-ever-finalized game Dragons, Archers, & Oxen. At the time I originally wrote the rules, DAO was a new game, but I really liked the idea of the Ox pushing pieces into elevator shafts, so I couldn't resist borrowing it.
The use of the terms Walking to denote making a single orthogonal step and Vaulting in reference to leaping three cells comes John William Brown's book Meta-Chess, although in both cases I did not maintain his exact meaning. Brown's definition of Walking is move without capturing only, but I preferred the name Walking Camel over Marching Camel, which would be the correct designation under his system. His definition of vaulting only applies to leaping three cells in an orthogonal direction. The Brown system would have required that I call the piece Vaulting Zooming Prince. Too long, I thought, and vaulting made much more sense, since the whole inspiration for the Prince's three-cell leap was the idea of it vaulting over empty elevator shafts.
Piece Values
If take Zillions' piece values and scale them so that the Pawn is worth 1 point, we get the following:
1.0 - Pawn
2.7 - Prince
2.8 - Camel
3.1 - Knight
3.2 - Ox
3.5 - Bishop
4.1 - Rook
7.1 - Queen
The numbers that are most suspect here are those for the Bishop and Ox. Zillions is known for placing too much emphasis on mobility of pieces, so that the number of cells that the Ox can reach probably inflates its value in Zillions' eyes. While the Ox is fairly mobile, its capturing power is much more limited, and the fact that it can not move to an adjacent cell without capturing or pushing is a big liability. Furthermore, the Ox is a piece whose value goes down as the game progresses because there are less pieces for it to push - it has been my experience that in the endgame the Ox is worth less than Knight, Camel, or Prince. The Ox is most dangerous in the beginning of the game, especially if a player moves too many pieces onto one level at once, where they can not all get out of the way fast enough if an Ox comes pushing through. The Bishop's value is in part determined by whether or not the player owning the Bishop has any Oxen left, since once all the Oxen are gone the Bishop becomes colorbound until the player can promote a Pawn to Ox. I am not sure how much, if at all, Zillions accounts for the presence of Oxen when valuing the Bishop.
On the other hand, Zillions' numbers match my own evaluation of the pieces fairly well. It gives a range of only half a Pawn from Prince to Ox, and indeed I have found those four pieces to be very close in value, depending on the situation. Since the non-Vaulting Prince and non-Walking Knight are about equal in value, and capturing Walking power is definitely worth more than non-capturing vaulting power, it makes sense that the Knight is worth more. And since the non-Walking Camel is definitely worth less than the non-Walking Knight, it would be logical for the Walking Camel to be worth less than the Walking-Knight. In this case, though, the single step improves the Camel much more than it does the Knight, since it changes the Camel from a piece that is colorbound to one that is not. The most difficult piece to gauge is still the Ox, since it has intangible benefits such as being able to push several pieces at once onto elevators in order to mobilize them faster.
I hope to provide more analysis and some sample games in the near future. In the meantime, readers are welcome to send comments and suggestions.
This game is copyright 1998, 2002 by Benjamin C Good. Marketing inquiries are welcome.
Written by Benjamin Good.
WWW page created: Thursday, August 22, 2002.
