RHINOS: A FAMILY OF
VARIANT CHESS PIECES
Introduction
Rhinos are a family of variant Chess piece that slide hippogonally -- David Parlett's term for moving in a Horse or Knight-like fashion -- without jumping. In addition to the basic Rhino, the family includes such variations as the single-step Rhino, the Mirror-Rhino and the Double-Rhino.
History
This family of pieces has been invented more than once. Ralph Betza invented the the TwiKnight or TwiKnight Double-Header(the Rhino), the KnightTwi (the Mirror-Rhino) and the Bronx (the Double-Rhino) for Confusion Chess in 1996. Ed Friedlander independently invented the Cubscout (the Rhino) for his Exotic Chess Applet. Peter Aronson then invented re-invented the Rhino Family in 2001. It all goes to show that you should pay attention to Ecclesiastes.
About the Name
The name Rhino is short of course for Rhinoceros, an animal that shares the Order Perissodactyla with Horses, but is rather harder to block than a Horse. Other names that were considered are the Heavy Horse and the Cataphract.
The names Rhino and Rhinoceros have been used before. Ed Friedkin uses the Rhino as the name of a piece that moves like a Queen, but pushes other pieces instead of capturing directly. Gollon Gives the name Rhinoceros for a piece from Shantranj Al-Kabir (Great Chess, but not the same as Turkish Great Chess), which moves like a Knight or a Bishop. However, as neither of these usages are common, there should be little confusion between those and the Rhinos described here. However, Ralph Betza's names do have precedence.
The Basic Move
The Rhino's basic move came from combining the movement of the Xiangqi Horse or Mao with that of the Wazir. This yields a piece that moves one square orthogonally, and then optionally, only if the first square was empty, one square diagonally outward, as in this diagram:
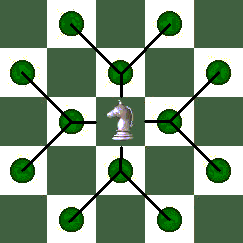
The Sliding Move
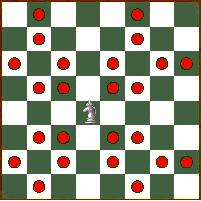
The Rhino's sliding move is similar to the alternating move of the Crooked Bishop: the Rhino slides one square orthogonally, then one square diagonally outward, then one square orthogonally in the first direction again, then one square diagonally outward in the second direction again, and so on until an opposing piece is encountered, the edge of the board is reached, or the player decides to stop moving. The following diagram shows the squares a Rhino can reach:

Mirror Rhinos
Mirror-Rhinos and one-step Mirror-Rhinos move the opposite of Rhinos: first diagonally, then orthogonally outward. The basic piece is a combination of the Fairy Chess Moa and the Ferz: one square diagonally, and then optionally, only if the first square is empty, one square orthogonally outward. As in this diagram:
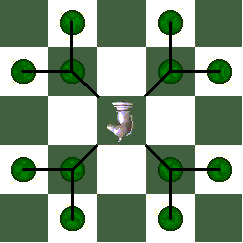
The one-step Mirror-Rhino becomes a Mirror-Rhino in pretty much the same way a one-step Rhino becomes a Rhino: first the Mirror-Rhino (or KnightTwi -- z[FW] in funny notation) moves a square diagonally, then a square orthogonally outward, then diagonally again in the first direction, then orthogonally outward again in the second direction, and so on until an opposing piece is encountered, the edge of the board is reached, or the player decides to stop moving the piece. The following diagram shows the squares a Mirror-Rhino can reach:
The Double Rhino
The Double-Rhino is a combination of the Rhino and the Mirror-Rhino. Ralph Betza called it the Bronx (z[WF]z[FW] in funny notation). It can reach the squares shown in this diagram:
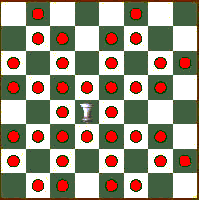
The Monster
The Monster is a combination Double-Rhino and Queen (RBz[WF]z[FW] in funny notation). It is a rather extreme piece, able on an empty eight by eight Chess board to reach all but eight squares:

Mating
On an eight by eight Chess board, I don't believe a Rhino or a Mirror-Rhino plus a King can mate a King, but a Double-Rhino plus a King can. A Monster should be able to mate unaided.
Rhinos vs Nightriders
While a Rhino can reach twice as many or more squares than a Nightrider, their relative value is unclear, since much of a Nightrider's value lies in its ability to jump over obstructing pieces, and to attack pieces behind lines of Pawns. It seems to me that depending on the situation, either a Rhino or a Nightrider might be the more valuable. Rhinos are, of course, more clearly more valuable than Maoriders.
Uses for these Pieces
I don't think I have figured out the best use of these pieces yet. Interestingly, one of my correspondents thought that Rhinos would work best in large variants, while another thought because of their ability to work around holes, Rhinos would work well in small variants. So far, they seem at least slightly awkward anywhere I've tried them, but I believe that there is a place for them in some game somewhere.
Zillions of Games
I have written a ZRF with a bunch of games featuring various types of Rhinos. None of them seem especially interesting on their own, but collectively they do illustrate how Rhinos move and how they interact with other pieces. It also provides examples of how to implement zig-zagging pieces such as Rhinos or Crooked Bishops without duplicating moves (duplicating moves messes up Zillions piece valuations).
It now includes both Ralph Betza's Confusion Chess 1, beta, and Confused Massacre, which is the Confusion Chess array vs the FIDE array.
You can download it from here:
Written by Peter Aronson.
WWW page revised: April 16th, 2001.
