Sequence of Fibonacci-Lucas Chess Design Games
Introduction
Fibonacci and Lucas numbers are numbers which obey the respective mathematical recurrence relations: Fn=Fn-1 + Fn-2, with F0=1, F1=1 and Ln= Ln-1 + Ln-2, with L1=1, L2=3, n=1,2,3...
Example: the first 10 Fibonacci numbers are: 1,1,2,3,5,8,13,21, 34,55. That is; each Fibonacci number Fn is the sum of its two successive preceding numbers Fn-1, and Fn-2. These numbers have many interesting properties and applications and many elements in nature obey them. Example: The rabbits and bees reproduction, the pineapple design, etc... In this article, I will design and develop new chess games based on Fibonacci and Lucas numbers.
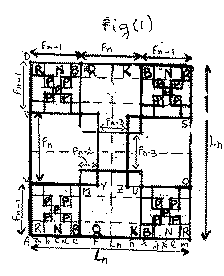
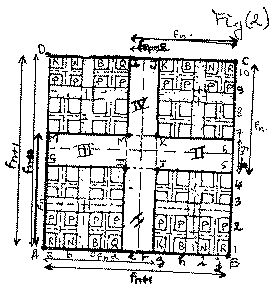

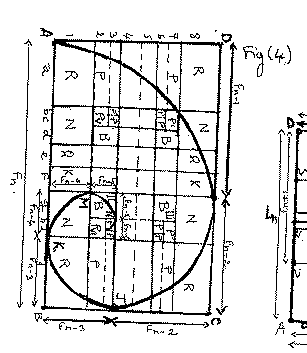
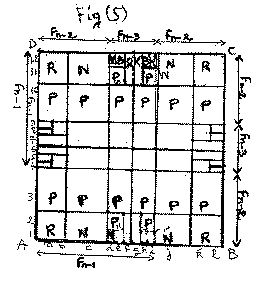


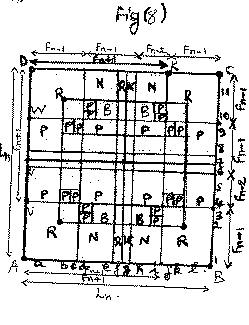
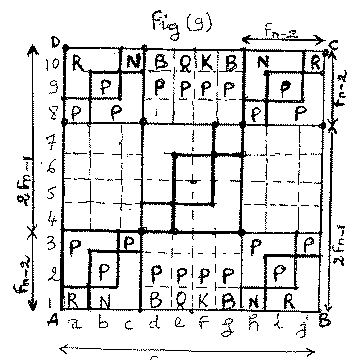
The diagrams of fig(1), fig(2), fig(3), fig(4), fig(5), fig(6), fig(7), fig(8), and fig(9) represent nine distinct chess games with pieces(pawns) initial arrangement, and where the sides obey the Fibonacci , or Lucas numbers, or both. Fig(1) is a 14x14 Lucas-Fibonacci chess game. Fig(2) is a 10x10 squares Fibonacci chess game. Fig(3) is a 12x12 Lucas-Fibonacci chess game. Fig(4) is a 8x10 Golden rectangle Fibonacci chess game. Fig(5) is a 11x11 Cyclic rectangles Fibonacci chess game. Fig(6) is a 12x12 Lucas-Fibonacci chess game. Fig(7) is a 10x10 two handed Fibonacci chess game. Fig(8) is a 11x11 cyclic rectangle Fibonacci chess game. Fig(9) is a 10x10 Lucas-Fibonacci chess game. Now, except for the chess game of fig(7), the rules of play for the other chess games are almost similar to those of the usual 8x8 squares chess with the addition that the Pawn can either move forwards, or horizontally one square, and it captures diagonally. Each chess game has its number of Knights, Rooks, Bishops, Queens and Pawns. Because of the nature of the chessboard designs (fractal items designs), the process of identifying the files is as follows.
For example: consider the 12x12 Lucas-Fibonacci chess game of fig(3). The chessboard squares coordinates are (x,y) with x=a,b,c,d,e,f,g,h,i,j,k,l, and y=1,2,3,4,5,6,7,8,9,10,11,12. The quadrangles I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII, XIII, XIV, XV, XVI, XVII, XVIII, XIX, XX, XXI, XXII, XXIII have the respective coordinates a1, d1, h1, k1, k4, d4, a4, a8, d8, h8, k8, k12, h12, d12, a12, a6, j6, j7, a7. The remaining quadrangles can be easily identified. The sides of the chessboard are Fibonacci, or Lucas numbers or both. Example, for fig(3), the chessboard is a square ABCD with sides equal to Fn-1 + Fn-2 + Fn-1, and DW=XC=CU=VB=BS=ZA=AL=Fn-1, and WX=UV=ZS=NL= Fn-2, and QR=MN=Ln-2. Where Fn are Fibonacci numbers and Ln are Lucas numbers. The castlings are like those of the 8x8 squares chess.
Now, concerning the chess games of fig(2) and fig(7) there are some special aspects to consider. Thus for the 10x10 Fibonacci chess game of fig(2), all pieces (except the pawn) must cross the central square IJMK (which comprises four sub squares) in order to reach one or the other side of the opponent fields. The pawns move from square to square. In other words, the zones I, II, III, IV constitutes barriers. Concerning the 10x10 two Handed chess game of fig(7), the game is as follows: white pieces have the fields DKEU and UAJF, and black pieces have the fields HKCI, and GIBJ. White pieces on QKEU move towards the opponent field GIBJ and vice-versa. White pieces on the field KCIH move towards the opponent fields AUFJ(see arrows on fig(7)). The white pieces(pawns) on DKEU cannot cross the segment KH, and the pieces on AUFJ cannot cross the segment FJ . Similarly, black pieces on KCIH cannot cross the segment KH, and those on the field GIBJ cannot cross the segment FJ. In addition, the pawns on the column 10,9, and 8(for white) can either move forwards or horizontally one square at a time in order to move forwards through the column 7 towards the opponent field. Similarly, the pawns on the columns a, b,c and d can move horizontally or vertically in order to be on the column e and to move towards the opponent field. This also applies for black pieces on the columns 1,2,3 and 4, and j,i,h and g. The castlings are like those of the 8x8 squares chess. In order to reach the opponent fields, all pieces(pawns) must cross the square EFGH which comprises four sub squares, called the central squares. For the chess game of fig(9), white pawns on b2 must move to the square c3 and then he can continue moving forwards along the column c towards the opponent field. This also applies for the pawn on the square i2. Similarly, black pawn on the square b9 must move to a8 and then he can continue moving along this column. This also applies for the pawn on i9 who must move to h8 and then continue along this column. Now all the nine chess games have fractal designs, since their items can be repeated similarly (see the book Fractal everywhere by B. MANDELBROT). The chess game of fig(4) can be called 10x8 FIBONACCI GOLDEN SPIRAL CHESS GAME.
Conclusion
Using Fibonacci and Lucas numbers, I have designed and developed new chess games which have fractal nature. All these above mentioned chess games can be simply called FRACTAL SEQUENCE OF FIBONACCI -Lucas CHESS GAMES
Written by A. Missoum.
WWW page created: April 16, 1998.
