Tetrahedral Chess
by J. Mark Thompson
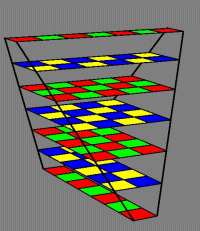
The inspiration for Tetrahedral Chess sprang from the contest for a chess variant on a board of 84 squares. Being a math junkie, I noticed that 84 is a tetrahedral number: the number of spheres stacked in a triangular-based pyramid, seven spheres on an edge. This suggested the possibility of making a 3-dimensional chess variant with a tetrahedral form. The opposing armies could begin on opposite edges of the tetrahedron, and the pawn rows could then completely enclose the pieces, so that play would begin with pawn development, as in usual chess.
The board
When a tetrahedron is sliced on a plane perpendicular to the line connecting the midpoints of opposite edges, the cross section is a rectangle. The Tetrahedral Chess board therefore consists of seven rectangular levels, as shown above in perspective. The rest of the diagrams here show the board as it appears in my ZRF, expanded vertically so that every square is visible.
Since the grid is not cubic, it's necessary to define the directions in which squares are adjacent to one another. There are twelve directions, corresponding to six lines going through each cell, one line parallel to each edge of the tetrahedron. Two of these lines remain on the cell's own horizontal plane (corresponding to directions north/south and east/west) and four extend up and down. The first diagram below shows the twelve cells in blue adjacent to a central red cell; a king on the red cell could move to any of the blue cells. The second diagram shows the lines extended to the end of the board: a rook on the red cell could move to any of the blue cells. It's interesting that a Rook on any square of an unoccupied Tetrahedral Chess board commands the same number of squares (18). The same observation applies in usual Chess, of course, where a Rook always commands 14 squares.

If you were to look straight down at the board, the squares on two adjacent levels would not coincide: the center of any square is directly below the corners of four squares on the level above. This is how it happens that there are four squares adjacent to each square above and below.
The squares of the board are colored in four colors: red, green, blue, and yellow, as shown in the third diagram. There are 23 red squares, 21 green, and 20 each of blue and yellow. These colors are conceived as having "temperatures": two of them (red and yellow) are "warm," the other two (blue and green) are "cool." Temperature will become significant in the definition of the Pawn moves and captures. Notice that no square is adjacent to any other square of the same color. The squares in any straight line of cells alternate between two colors, as shown below (the yellow-and-green line is marked for greater clarity).

I go over this at some length because visualizing the geometry of the board is the hardest thing about understanding Tetrahedral Chess. Although the tetrahedral grid is difficult to visualize, it has an advantage of simplicity over the usual 3-dimensional cubic grid, which has six orthogonal, twelve diagonal, and eight triagonal directions extending from any cube: 26 directions in all, compared with only 12 in Tetrahedral Chess.
Board notation
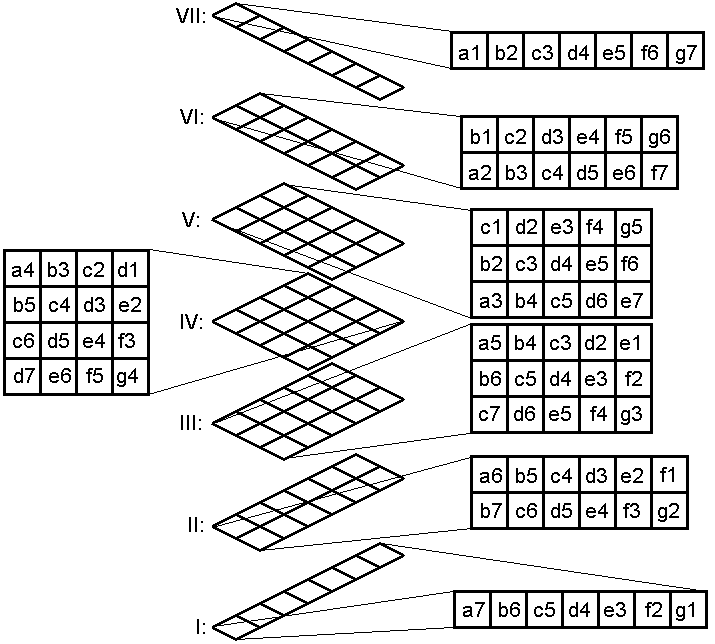
A board notation is shown above. The cells on each level have the labels shown in the fly-outs, where the lines indicate which edge of the fly-out corresponds to which edge of the level in the 3-D diagram. The full notation for a cell is the Roman numeral indicating its level, followed by the letter and number indicating the square. For instance, the four corners of the board are Ia7, Ig1, VIIa1, and VIIg7.
The pieces
There are five kinds of pieces in Tetrahedral Chess, counting Pawns: King, Rook, Knight, Dababante (shown as a Bishop), and Pawn. Their moves are derived from the moves of analogous pieces in usual Chess.
The Rook
![]()
Starting with the simplest: a Rook moves any number of squares in any one of the 12 directions, until it is stopped by a piece or the end of the board. Examples of the Rook move are shown in the illustrations above, so rather than repeat them here I'll save my illustrations for the harder pieces.
The King
![]()
The King, which is royal, moves to any adjacent square in any of the 12 directions. Therefore it can only move to a cell of a different color. A King cannot capture a Dababante or a Rook; it can capture a Pawn or a Knight. (Note: this is a change from my earlier conception, in which a King could not capture a Knight.) Nor, however, may a King move to any square where the enemy King could move on the next turn. The King's usual move is also illustrated above.
Also, the King may castle as in usual Chess: that is, the King moves two squares toward one of the Rooks, and the Rook moves toward and passes the King, to the next square. The usual castling conditions hold: a player may only castle if neither the King nor the Rook has moved before, and only if the King is not in check, and only if the square over which the King moves is not under attack.
The Knight
![]()
The squares to which a Knight can move are those satisfying the following:
- A King could move there in two moves, if we ignore any other pieces on the board.
- A King could not move there in one move.
- Its color is different from the Knight's starting square.
Therefore a Knight cannot move to any square on the same level as the one where it originates. If there is room on the board, it can move to eight squares on the levels immediately above or below, and to four cells on the next-removed levels. Here are two examples of the squares to which a Knight moves, from cell IVd3 and IIId4:

Each player begins with one Knight, but it is off the board (a "pocket Knight"). A player may use a turn to drop the Knight onto any vacant square on the three levels nearest the player's home level, after which it moves as described above.
The Dababante
![]()
A Dababante is represented by a Bishop because its usual move is color-bound. The name Dababante is used in chess variants to refer to a piece that moves in orthogonal lines but only to every other square. Similarly here, a Dababante (in its usual move) moves in any of the 12 directions, but only to the squares of the same color as its starting square. Any pieces, friendly or enemy, in the intervening squares are jumped over, except for Pawns: a Dababante cannot move through a square containing a Pawn. If the four Dababantes shown in the illustration below were alone on the board, each could move to the squares shown. Notice that a Dababante in a corner cell commands more squares than in any other position.

However, the Dababantes are not completely color-bound, because a Dababante can also move onto any square adjacent in any of the 12 directions (a King move), as long as the player has no Dababantes on that square's color already.
A player's Dababantes begin two on red, two on green. Hence at the start, any of these Dababantes could move to an adjacent yellow or blue square. But once the player moves one to, say, a blue square, none of his Dababantes would be able to move onto adjacent blue squares, until the Dababante on blue either moves to another color or is captured.
A result of this rule is that when a player loses a Dababante, his remaining Dababantes become stronger. In an endgame study included with my ZRF, I convince myself that a King and a single Dababante can checkmate a bare King. I'd be interested in knowing if my play for Black was flawed in a way that invalidates this opinion.
The Pawn
![]()
A Pawn may move (without capturing) to a forward-adjacent square whose color is the opposite temperature from the color of the Pawn's starting square; it may capture to a forward-adjacent square whose color is the same temperature as its starting square.
Hence a Pawn which starts on blue may move (without capturing) to red, then to blue again, and so on. One that starts on yellow may move from yellow to green, to yellow, and so on. Most Pawns have two choices of squares whither they may move, although the Pawns at the edges of the starting lineup (as a consequence of the rule given above, and the geometry of the board) have only one. A Pawn on blue may capture an enemy piece on green, or from green to blue, red to yellow, or yellow to red.

In the illustration above on the left, the White Pawn (since it stands on a green square) can move to either of the yellow squares, or it can capture either of the Black Pawns on the blue squares. If the Black Pawns were on the yellow squares, the White Pawn would be blocked. On the right, the Black Pawn on the green square cannot move, because the two yellow squares to which it might move are blocked by the Black Pawn and the White Dababante. The Pawn on the green square guards one of the Pawns on the blue squares (the one nearer the Dababante). The Pawns on yellow and red squares attack one another.
When a Pawn reaches the farthest level, it promotes to any piece.
As stated above, a Pawn is the only piece that can block a Dababante. Pawns and Knights are the only pieces that can be captured by a King.
There is no double-step, and consequently no en passant capture.
The starting position
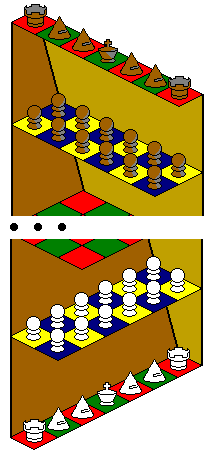
The pieces begin, White on level I, Black on level VII, in the order Rook - Dababante - Dababante - King - Dababante - Dababante - Rook. Twelve Pawns occupy all the squares of the next levels, the White Pawns on level II and the Black on level VI. Each player also has a Knight in pocket at the start of the game.
Acknowledgments
The idea of a Pocket Knight comes from Pocket Knight Chess, of course, and provided a convenient way to add Knights to this game in spite of limited space in the opening row. The two-dimensional form of the Dababante seems to have been invented by V. R. Parton for Dababante Chess. It was when I read R. Wayne Schmittberger's description of 3D Hook-Move Chess in his New Rules for Classic Games that I first became aware of the difficulty of achieving checkmate in the usual cubic-grid 3-D chesses, and which also planted in my mind a general dissatisfaction with the cubic grid as a basis for 3-D chess. The tetrahedral numbers are described in The Penguin Book of Curious and Interesting Numbers, by David Wells, and form the fourth diagonal of Pascal's Triangle.