Coherent Chess
Coherent Chess is a chess variant, invented by Carlos Cetina from México. The idea behind the variant is that each piece has a movement rule without peculiarities like en-passant, castling, etc.
Rules
Coherent Chess is played on a board of nine by nine squares. Each player has a king, two queens, two rooks, two bishops, two knights, and seven pawns.
The starting setup of the game is as follows:
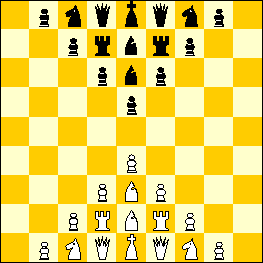 White:
White:
King e1; Queen d1, f1; Rook d2, f2; Knight c1, g1; Bishop e2, e3; Pawn
b1, c2, d3, e4, f3, g2, h1.
Black:
King e9; Queen d9, f9; Rook d8, f8; Knight c9, g9; Bishop e8, e7; Pawn
b9, c8, d7, e6, f7, g8, h9.
Movement of pieces
Kings, queens, rooks, and bishops move in the same way as in orthodox chess (but there is no castling.)
Pawns move as kings (but without being affected by check themselves), i.e., one square in an arbitrary direction. Pawns do not promote.
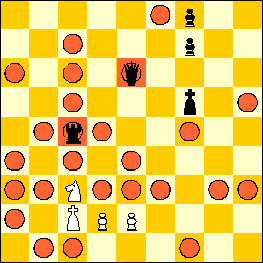
The movement rule of the knight is the following: first, the knight moves one or more squares like a rook or a bishop, and then the knight moves the same number of squares like the other of the two (bishop or rook.) So, the knight has the following options:
- First, it moves a number of squares as a rook. Then it makes a corner of 45, 135, 225, or 315 degrees, and then moves the same number of squares as a bishop. All squares that are passed by must be empty, i.e., unlike orthodox chess, a knight in Coherent Chess does not jump over pieces.
- First, it moves a number of squares as a bishop. Then, it makes a corner of 45, 135, 225, or 315 degrees, and then moves the same number of squares as a rook. Again, all squares passed by must be empty.
See below for an example. (The white knight has the possibility to take the rook or the queen.)
Other rules
The purpose of this game is to mate the opponents king: check, mate, and stalemate are the same as in orthodox chess.
Comments
The bishops location is chosen such that they start the game on squares of a different color. About having two queens, the inventor writes:
Why are there two queens by side? For the same reason that there are two rooks, two bishops and two knights!
The clue to this game seems to master the knights, that gain more and more power when the board gets empty.
Carlos Cetina invites readers to play a game of Coherent Chess against him by email: write to (email removed contact us for address) s.ujat.mx.
Sample Game
White: Dimitry Valencia Villahermosa, Mexico Black: Carlos Cetina January 25, 1998Comments by Carlos Cetina
1.Pd3-d4 Pb9-b8 2.Pb1-b2 Ph9-h8 3.Pf3-f4 Pc8-c7 4.Pb2-b3 Ph8-g7 5.Pg2-g3 Pd7-d6 6.Ng1-g2[Path: g1-h2-g2]
6. ... Be8-d7 7.Ph1-h2 Pf7-e8 8.Be2-d3 Pg8-f7 9.Pf4-f5 Pf7-f6 10.Pb3-c4?[Better: 10.Pg3-g4 or 10.Pf5xe6]
10. ... Pf6xf5 11.Pe4xf5 Pe6xf5 12.Qd1-h5 Pg7-g6 13.Qh5-e2 Bd7-c6 14.Ng2-i1[Path: g2-h1-i1]
14. ... Ng9-g7[Path: g9-i7-g7 or g9-i9-g7]
15.Pg3-g4 Pf5xg4 16.Qe2xg4 Pe8-f7 17.Ph2-g3 Rf8-i8 18.Ni1-g1[Path: i1-i3-g1]
18. ... Be7-i3 19.Pg3-h2 Bi3-e7 20.Rd2-e2 Pd6-e6 21.Be3-d2 Pe6-f5?[Better: 21. ... Qf9-i6]
22.Bd3xf5! Ri8-e8?[Preferable: 22. ... Qf9-h7 or 22. ... Pg6xf5 23.Bd2-h6 Pf5xg4 24.Bh6xg7+ Pf7-f8 (not 24. ... Ke9-e8? 25.Rf2xf7 Qf9xf7?? 26.Qf1xf7+ with strong attack, and 26. ... Ke8xf7 is not possible because of the c1-knight protects to f7-queen by the path c1-f4-f7) 25.Re2xe7+ Rd8-e8 following by 26. ... Qf9-g9]
23.Bf5xg6! Be7-a3?[Preferable: 23. ... Pf7xg6 24.Rf2xf9+ Ng7xf9 25.Qf1xf9+ Ke9xf9 26.Qg4-i6+ Re8-g8 27.Re2xe7 Rd8-e8]
24.Bg6xf7! Ng7xf7[Without comments! Path: g7-g6-f7 or g7-g8-f7 or g7-f6-f7 or g7-f8-f7]
25.Rf2xf7 Re8xe2+ 26.Qg4xe2+ Rd8-e8 27.Rf7xf9+ Ke9-d8 28.Bd2-g5+ Kd8-c8 29.Rf9xd9 Nc9xd9[Path: c9-d8-d9]
30.Qf1-h3+ Kc8-b7 31.Ng1-e5?![Path: g1-g3-e5 or g1-e3-e5; Why not 31.Qh3xa3?]
31. ... Ba3xc1 32.Qh3-b3+ Pc7-b6 33.Pc2xc1 Re8xe5 34.Qe2xe5 Nd9-h7+[Path: d9-f9-h7 or d9-f7-h7; it is giving check at the same time by the paths h7-h4-e1 and h7-e4-e1]
35.Ke1-d2 Pb8-c7 36.Ph2-g3 Bc6-h1 37.Pc1-c2 Nh7-f7[Path: h7-f9-f7 or h7-f5-f7]
38.Qe5-e1 Nf7xg5[Also it moves as normal, usual, FIDE-knight!]
39.Qe1xh1+ Kb7-c8 40.Pc4-c5 Pb6-b7 41.Pg3-f4[Of course, 41.Qh1xb7+?? Pc7xb7. Also, 41.Qb3-g8+?? Ng5xg8+ (path g5- d5-g8 or g5-d8-g8) giving check by g8-g5-d2, not by g8-d5-d2 due to d4-pawn obstructs this path]
41. ... Ng5-i5??[Path: g5-i3-i5 or g5-i7-i5. Black loses his knight by 42.Qh1-i2+ Ni5xi2 (path i5-f5-i2 or i5-f2-i2) 43.Qb3-h3+]
42.Qb3-f3?![Fortunately, White is some inattentive!]
42. ... Pb7-b8??[Unfortunately, Black also is enough inattentive!]
43.Pc2-c3 Kc8-b9 44.Pc3-c4 Pc7-c8 45.Pc4-d5 Pc8-c9 46.Kd2-c3 Kb9-a9 47.Pd5-d6 Ni5-c8[Path: i5-f5-c8 or i5-f8-c8]
48.Kc3-b4 Nc8-c2+[Path: c8-i8-c2 or c8-i2-c2]
49.Kb4-a4?[Better: 49.Kb4-b3]
49. ... Nc2-b2+[Path: c2-c1-b2 or c2-c3-b2 or c2-b1-b2 or c2-b3-b2]
50.Ka4-a5?[Again, it was better 50.Ka4-a3]
50. ... Nb2-a2+[Path: b2-b1-a2 or b2-b3-a2 or b2-a1-a2 or b2-a3-a2; it is giving check by the path a2-d2-a5]
51.Ka5-b6[Also it is possible both 51.Ka5-b5 and the surprising move 51.Pd4-c3!, obstructing the d2-a5 diagonal. Note the c5 pawn is "fixed", since that if it for instance moves toward b4, then the a2-knight would give check by a2-d5-a5. Note also that the a2-knight controls the squares a4 (paths a2-c2-a4 or a2-c4-a4), b4 (as normal knight) and a6 (path a2-e2-a6)]
51. ... Pb8-a7+[This pawn is protected by the knight by the path a2-f7-a7]
52.Kb6-c7??[Decisive error. 52.Kb6-b5 is the correct and practically unique move. Note the knight controls the c6-square by the path a2-a4-c6]
52. ... Pc9-d8 checkmate!!![This pawn is protected by the knight by the path a2-a5-d8]
The morality of this sample game is:
"Playing Coherent Chess never resign none game... until the end, until your adversary gives you checkmate!"
Written by Hans Bodlaender, based on emails of Carlos Cetina. Sample game and analysis by Carlos Cetina.
WWW page created: January 28, 1998. Last modified: March 27, 1998.
