Prince
By Gavin Smith
Graphics by Gavin Smith and L. Lynn Smith
The Basic Idea:
Chess is essentially a geometric, mathematical game played on a two-dimensional field.
This outline tries to answer the question "What would it be like to expand the same game to a three-dimensional field?".
This is not an attempt to improve on Chess. Fully expanding it to three dimensions makes it a much more complicated game.
There are other ways to answer the questions posed here, but this outline tries to keep as true as possible to the concepts in Chess,
using them as a model.
See Appendix F for a quick reference.
The "History" of Prince:
As of this writing, May 18th, 2007, there is little history of Prince. Chessvariants was the first to post any definition of this game on May 13th, 2004. I thought it up going stir crazy recovering from surgery in March of that year. Though I wasn't aware of any other 3-D chess variants, other than hearing that someone had made the game on "Star Trek" real, I figured _someone_ must have done something like this before. Sure enough, I later found Chessvariants.com, was surprised to find my idea was as unique as it was, typed this up, sent it off to the editors, and here we all are.
In the following months, L. Lynn Smith (no relation), Joe Joyce and I play tested it, though we didn't finish a game. L. Lynn Smith put together the ZOG implementation (thank you very much!). I also incorporated some of his suggestions in the initial set up and subtleties of how blocking works for some planar movers. Revisiting the concept now after a couple of years, I have not changed any rules, but have shortened their explanation and added graphics (thank you, Tony!).
The previous variant most similar to Prince is 3d8l, in that it also gives each player 128 pieces each on an 8x8x8 field. However, in addition to all the pieces in 3d8l, Prince also uses "planar" movers, many of which are similar to the pieces previously described by Chris Witham, whose planar Rooks and Bishops I discovered on Chessvariants.com after I had arrived at a definition for them myself. Prince defines how to block these planar movers differently than Mr. Witham, in addition to having kinds of planar movers not previously defined.
I am currently figuring out how or whether to pursue a copyright or patent, whichever is appropriate (I have already sent a copy of this to myself via registered mail), and would welcome any advice on the subject. In the mean time, feel free to distribute this outline, as long as it is passed along that no one tries to make any money off it without my permission, and gives me credit for thinking it up.
Please also feel free to play this game, perhaps tinkering with the opening positions of the pieces if you think you can come up with something better. I also haven't figured out for sure where, for example, the players should sit or how the field should be oriented. Have fun, if indeed that's possible with this game, and let me know!
The Basic Rules:
Prince shares all the same basic rules with Chess:
There are two players that begin with the same number of pieces in the same positions on opposite sides of the field. One player's pieces are "white" and the other player's are "black". "White" always moves first, and the two players alternate taking turns from there. Each turn consists of a player moving exactly one of his or her own pieces once. No two pieces may ever occupy the same space in the field, and if a piece is moved to a space occupied by an opposing piece, the opposing piece is "captured" and removed from the field.
Each player has one King. One player wins by capturing the opponent's King, ending the game. Actually the game ends with "check mate", meaning a player's King cannot avoid capture on the opponent's next move (even if, hypothetically, the King were to not move).
A player must move a piece on every turn. If a player may not legally move any piece on his or her turn, and the player is not in "check mate", the game ends and is considered a tie, or "stale mate".
A tie may also occur if neither player can capture the other's King. This is ruled to be the case if, on three separate turns, the position of all pieces of both sides is exactly the same, as well as the possible next moves of all of these pieces (including castling and capturing "en passant"). A game in Chess is also considered a tie if a certain number of turns go by without either player capturing a piece or moving a Pawn. For now, I suggest this number of moves in Prince be 100. But if anyone comes up with a check mate scenario requiring more moves than this, please let me know.
The Pieces:
Some things that all pieces in Chess and Prince have in common not already mentioned:
They all occupy exactly one space on the field. They all have the potential to move. They also all have the potential to capture opposing pieces. With the exception of the Pawn, discussed later, a piece may capture any opposing piece that occupies a space it may move to, and does so by moving to that space. Another way to say this is that it captures the same way it moves.
Defining How Pieces Move:
In Chess, pieces move by changing their position on the field. To put it in mathematic terms, they change their position value. On a two-dimensional field, a position value has two numbers: A column number and a row number. These rules will also refer to these numbers as dimension values. Setting aside the traditional alpha-numeric notation for position in Chess, we may think of the column farthest to the left of "white" as he or she faces the board as column 1, and the column farthest to the right as column 8. The row nearest "white" may be row 1, and the row nearest "black" may be row 8. For Prince in three dimensions, a position value has three dimension values: A column number, a row number, and a tier number, with each column, row, and tier in the field numbered 1 through 8.
As in Chess, a Rook in Prince is defined as a piece that may change one and only one of its dimension values. This motion is blocked by other pieces in the field, whether of the same or different "color". To understand how this may occur, we can think of the Rook as changing the dimension value in question incrementally, that is to say, moving one space at a time, taking the fewest number of moves, or shortest "path" possible to reach its destination space. This will mean moving in one direction along a straight line. If any other piece occupies any of the spaces in this shortest "path", then the Rook is blocked and cannot move to the destination space.
The Great Schism:
When we try to define a Bishop in Prince, using Chess as a model, there are two viable alternatives. One is that a Bishop in Prince, as in Chess, changes exactly two of its dimension values by the same amount. The other is that, as in Chess, it must change all of its dimension values by the same amount.
The Bishop in Prince will be defined as a piece that must change two and only two of its dimension values, and by the same amount. Note that "change" may mean "add to" in the case of one value and "subtract from" in the case of the other value in the same move. But two values must be changed, and by the same amount (in terms of absolute value). It may choose which two values to change. This means that a Bishop in Prince may move in up to twelve different directions. This move may also be blocked, and again we determine this by thinking of the Bishop as making incremental moves, which in the case of the Bishop means changing two values by one with each incremental move. Again, the Bishop must take the shortest path possible, which will be a straight diagonal line, and if any other piece occupies any space along this path, the move is blocked. Note that as in Chess, if the sum of the dimension values of a Bishop is even, it can only move to similarly "even" spaces. Similarly, if the sum is odd, it can only move to "odd" spaces. The Bishop cannot escape this restriction throughout the entire game. So it is recommended that a Prince field, like a Chess board, have the "odd" spaces be light and "even" spaces be dark.
Prince introduces the Merchant, which is the alternate definition of a Bishop in three dimensions. Like the Bishop in Chess, a Merchant must change all of its dimension values by the same amount. This means it can move in up to eight different directions. The same rules regarding blocking apply as for the Rook or Bishop, with the incremental moves considered being Merchant moves, changing all three values simultaneously by one.
The Merchant is even more restricted than the Bishop in terms of where in the field it can ultimately move. It will only ever be able to visit one out of four spaces in the field. So it is recommended that a Prince field have four colors: gray, blue, red, and green. Note that half of all spaces of each color will be odd, or light, and half will be even, or dark, making eight colors recommended for the Prince field.
For a mathematic explanation of Merchants' restriction, See Appendix A. See Appendix E for illustrations.
The King may move one space as either a Rook, a Bishop, or a Merchant. As in Chess, it has the special restriction that it may not move to a space that would allow the opposing player to capture it on the next move, which is called moving into check.
The Pawn may move only like a Rook, but may capture only like a Bishop or Merchant, with the following additional restrictions like those in Chess:
-With every move or capture, "white's" Pawns must add to their tier number; "black's" Pawns subtract from their tier number.
-A Pawn may only move one space on a turn, whether capturing or simply moving, except for its first move, when it may, if simply moving, move two spaces, if such a move is not blocked. For purposes of determining whether such a move is blocked, treat the Pawn as a Rook.
A caveat to this is that if a Pawn does move two spaces on its first move, and an opposing Pawn could have captured it if it had moved only one space, then the opposing Pawn may in fact capture the Pawn as if it had moved only one space. This capturing "en passant" as it is called, can only be done by an opposing PAWN, and only on the move immediately following the move of two spaces by the original Pawn in question.
If a Pawn ever reaches the opposite tier (Tier 8 for "white", or Tier 1 for "black"), as in Chess, it may immediately become any other kind of Prince piece other than a King.
The Diversification of Military Technology:
With the split of the Bishop into the Bishop and the Merchant, we similarly have the option to split the Knight. Just as Chess uses all basic ways an object can move through a two dimensional square grid, Prince tries to use all basic ways an object can move through a three-dimensional cubic grid. It also refers to different basic ways soldiers can move in the variations of the Knight thus created.
As in Chess, the Knight in Prince may move one space as a Rook, and one space as a Bishop. Both moves must be in the same "general direction", which is defined thus: The dimension value that is changed by the Rook move must be changed in the same manner (whether added to or subtracted from) in the Bishop move. For example, if it moves one tier up with the Rook move, then it must move another tier up, in addition to moving one column or row to either side, with the Bishop move. Also as in Chess, the Knight cannot be blocked.
The Captain moves one space as a Rook and one space as a Merchant, again in the same general direction, which again is defined similarly (i.e., the dimension value changed in the Rook move must be changed the same way in the Merchant move). It also cannot be blocked. Note that the Captain faces the same movement restrictions as the Bishop regarding odd and even spaces.
The Ace moves one space as a Bishop and one space as a Merchant. These moves must both, again, be in the same general direction, which in this case means that both dimension values changed in the Bishop move must be changed the same way in the Merchant move. The Ace also cannot be blocked.
The Marine may move as either a Knight or a Captain.
The Paratrooper may move as either a Knight or an Ace.
The Admiral may move as either a Captain or an Ace.
The Astronaut:
The Astronaut may move as either a Knight, a Captain, or an Ace.
Note that the Astronaut, similar to a Knight in Chess,
may move to any space two spaces away that neither a Rook, nor a Bishop, nor a Merchant could move to in a single turn, assuming an open field.
For additional explanations as well as illustrations of these "Knight" moves,
see Appendix B.
Polygamy:
Just as we can combine the moves of Knights, Captains, and Aces, so we can combine the moves of Rooks, Bishops, and Merchants.
In Chess, the only such combination mover possible is the Queen. In Prince, there are four.
The Court:
The Court, like the Queen in Chess, may move as either a Rook, or instead as a Bishop, on any given turn.
The Market:
The Market may move as either a Rook or a Merchant.
The Artist:
The Artist may move as either a Bishop or a Merchant.
Note that unlike the Bishop or the Merchant, the Artist may ultimately move to any space of the field.
The Queen:
The Queen in Prince may move as either a Rook, a Bishop, or a Merchant.
Two-Dimensional Movers:
One might think that we have exhausted all the possibilities of basic kinds of movement now that we have a translation of all the pieces in Chess,
or that at least nothing more could be added if we stick to Chess as a model.
However, just as there are two viable alternatives to defining Bishop movement in three dimensions,
so there are two viable alternatives to defining what it fundamentally means for a piece to move through three dimensions.
In Chess, the Rook, the Bishop, and the Queen move to points within a set of lines on a board.
That is to say, they move to points within a set of one-dimensional spaces on a two-dimensional space.
The analogous pieces we have so far defined also move to points within a set of one-dimensional spaces.
But since the space containing these lines has now expanded to three dimensions,
is it not equally viable to define these pieces as moving to points within a set of two-dimensional spaces,
2 being n-1 where n is the number of dimensions in the field?
This means defining how a Rook, a Bishop, and a Merchant, and their combinations could move to points within planes rather than just along lines.
The Base:
The Base is the planar extension of the linear Rook. A Base may move by changing any two of its dimension values.
Another way of defining this is that a Base is able to move to any space that can be reached by moving in any two directions in which a Rook may move.
It's range of motion then will be three planes, each containing two axes of Rook movement that intersect at the Base.
For purposes of blocking, we again think of the shortest possible path of incremental moves of the appropriate movement type.
However, for a destination space on a plane but not within a line, there are multiple possible shortest paths, each of equal length.
To make blocking effective then,
if any of the spaces on this plane in ANY of the shortest possible paths to a destination space is occupied by another piece,
then the destination is blocked and the Base cannot move to it.
See Appendix C.
The Scientist:
The Scientist is the planar extension of the Bishop. It may move to any space that can be reached by moving in two Bishop directions.
It's range of motion is a set of seven planes each of which have two (and some of which have three) axes of Bishop movement intersecting at the Scientist.
Similarly, a destination in one of these planes is blocked
if any of the spaces in any of the shortest possible paths of Bishop moves within this plane to the destination space is occupied by another piece.
Note however, that for the Scientist, as well as the other planar movers below,
there may be some destinations which lie on two or more planes which may be blocked on one plane, but not blocked on others.
Prince does not consider such destinations blocked.
If a plane on which a piece can travel can be found where the destination is not blocked,
meaning if two directions can be found where all shortest paths using those two directions are open, then the piece can move to the destination.
The blocking issues of different planes are considered independently, having no bearing on each other even if they intersect.
The destinations affected by this rule are alternate spaces along lines of Rook motion.
The Reporter is the planar extension of the Merchant. It may move to any space that can be reached by moving in two Merchant directions. Its range of motion is a set of six planes that each contain two lines of Merchant movement that intersect at the Reporter.
Blocking a Reporter's move works the same as for the Scientist, but considering shortest possible paths of Merchant moves instead of Bishop moves. Again, the blocking issues of different planes have no bearing on each other, even if those planes intersect.
The University may on a given turn move as either a Base, or instead as a Scientist. Again, the blockages of different planes have no bearing on each other, even if they intersect, and regardless of the type of plane. For combination planar movers in general, for any type of direction in which the piece can move, (Rook or Bishop for the University, e.g.), if two directions of that type can be found where all shortest possible paths to a space using those two directions are open, then the piece can move to the space.
The Network may move as either a Base or a Reporter.
The Spy may move as either a Scientist or a Reporter.
The Prince may move as either a Base, a Scientist, or a Reporter.
The Prince is an extremely powerful piece:
-A Prince may check mate an opposing King completely unassisted, without being threatened by the King.
-A Prince in the middle on an open field can choose to move to any of 355 spaces, more than two-thirds of the entire field of 512.
-From such a Prince, there are only three spaces in the entire field that an opposing King may be (or move to if it is the King's turn) to escape check mate on the Prince's next move.
-A Prince may check mate an opposing King on an otherwise open field in two moves, regardless of the initial position of the Prince and King.
There are no Princes at the start of the game. A player may only gain a Prince when a Pawn reaches the far tier.
The Field:
The field in Prince is an 8X8X8 cube. At the start of the game, each player has 128 pieces: 64 Pawns, 4 Rooks, 4 Bishops, 4 Merchants, 4 Knights, 4 Captains, 4 Aces, 2 Marines, 2 Paratroopers, 2 Admirals, 2 Astronauts, 4 Courts, 4 Markets, 4 Artists, 4 Queens, 4 Bases, 4 Scientists, 4 Reporters, 1 University, 1 Network, 1 Spy, and 1 King. "White's" Pawns take up the entire second tier, and "black's" Pawns take up the entire seventh tier. The rest of "white's" pieces are on the first tier, and the rest of "black's" pieces are on the eighth tier. They are both arranged the same way, on the same column and row numbers. What follows is my current suggestion, with column 1, row 1 at the bottom left:
Eighth Row: Base, Paratrooper, Knight, Rook, Market, Captain, Marine, Base.
Seventh Row: Admiral, Ace, Court, Bishop, Merchant, Artist, Ace, Astronaut.
Sixth Row: Captain, Artist, Queen, Scientist, Reporter, Queen, Court, Knight.
Fifth Row: Market, Merchant, Reporter, University, Spy, Scientist, Bishop, Rook.
Fourth Row: Rook, Bishop, Scientist, King, Network, Reporter, Merchant, Market.
Third Row: Knight, Court, Queen, Reporter, Scientist, Queen, Artist, Captain.
Second Row: Astronaut, Ace, Artist, Merchant, Bishop, Court, Ace, Admiral.
First Row: Base, Marine, Captain, Market, Rook, Knight, Paratrooper, Base.
Castling In Prince:
The King may "castle" two different ways, as in Chess. The King may castle near, or "King" side by moving the King to Column 2-Row 2, and moving the Base in Column 1-Row 1 to Column 3-Row 3, all in a single move. It may castle far, or "Spy" side by moving to Column 6-Row 6, and moving the Base at Column 8-Row 8 to Column 5-Row 5.
To castle near side, Column 2-Row 2 and Column 3-Row 3 must be unoccupied on the King's tier. To castle far side, Column 5-Row 5, Column 6-Row 6, and Column 7-Row 7 must all be unoccupied on the King's tier.
The same rules apply as in Chess in that in order to castle, neither the King nor the castling Base may have been moved (even if they have since moved back), the King may not be in check, and it may not "move through" check, meaning we must consider the King making incremental Bishop moves in the shortest possible path to the destination space (the space where the King ends up after the castling move), and no opposing piece, on the opposing player's next move, may be able to move to any of the spaces in this path.
For a quick reference of Prince, see Appendix F.
Prince Appendix A - Explaining the Limitations On Merchants:
If we consider a position value, writing it as (x,y,z) where x is the tier number, y is the column number, and z is the row number,
and consider the "evenness" of each of these values, we will notice the following eight possibilities,
each of which occur with the equal frequency on any axbxc field, where a, b, and c are even numbers:
1. (even, even, even)
2. (even, even, odd)
3. (even, odd, even)
4. (even, odd, odd)
5. (odd, even, even)
6. (odd, even, odd)
7. (odd, odd, even)
8. (odd, odd, odd)
Note that we can pair up these eight possibilities in the following manner, creating four subsets of position values:
1. All three dimension values share the same "evenness" (cases 1 and 8).
2. Only the tier and column values share the same "evenness" (cases 2 and 7).
3. Only the tier and row values share the same "evenness" (cases 3 and 6).
4. Only the column and row values share the same "evenness" (cases 4 and 5).
Now consider an incremental Merchant move.
A Merchant by definition must change all three of its dimension values be the same amount.
When a Merchant moves incrementally, i.e. one space, all three values are changed by one.
This will change the "evenness" of all three dimension values, whether the change for any given dimension is positive or negative.
Therefore whatever dimension values shared their "evenness" before will do so again, and whatever ones did not, again will not.
All Merchant moves can be thought of as being made up of these incremental moves.
Therefore whichever of the four subsets the position value of the Merchant belonged to before the Merchant moves,
the new position value of the Merchant after it moves must again belong to the same subset.
In this way a Merchant is trapped into only a quarter of the field for the entire game.
Note that this restriction is distinct from the odd and even restriction of the Bishop,
as all Merchants can travel to equal numbers spaces whose sum of dimension values is odd or even.
One math formula you could use to determine which of these four subsets a space belongs to without needing to compare is the following:
2*((x + y) MOD 2) + (x + z) MOD 2
This will give you the values 0, 1, 2, or 3 depending on which of the four subsets the space is in.
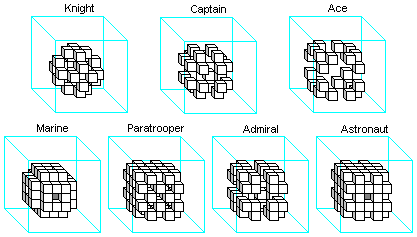
Prince Appendix B - Illustrating "Knight" Movers:
All of the "Knight" movers (the Knight, the Captain, the Ace, the Marine, the Paratrooper, the Admiral, and the Astronaut),
move by changing any one dimension by two, and either of the two other dimensions by one.
How they may or may not change the third dimension determines which kind of "Knight" the piece is:
The Knight must not change the third dimension, the Captain must change the third dimension by one, and the Ace must change the third dimension by two.
You can also describe these pieces as "jumping" from one corner to the opposite corner of an nxnxn space.
A Knight would be a 1x2x3 jumper, a Captain a 2x2x3 jumper, and an Ace a 3x2x3 (or 2x3x3) jumper.
Below are illustrations of where each kind of "Knight" may move if placed in the middle of the field at Tier 4, Column 4, Row 4.
Prince Appendix C - Illustrating Rook and Base Moves:
On an open field, the Base may move to any space that shares any of its dimension values.
Below is an illustration provided by L. Lynn Smith of the planes within which a Base may move
when placed in the middle of the field at Tier 4, Column 4, Row 4.

A destination space for a Base is blocked if any space is occupied by another piece where
all dimension values fall between the respective dimension values of the Base and the destination, inclusive.
Conversely, a piece on a field blocks all spaces from the Base where
the change of all the dimension values are all greater than or equal to the change of the respective dimension values between the piece and the Base,
and the directions of these changes (up vs. down, e.g.) are all the same.
Below are illustrations provided by L. Lynn Smith showing examples of how this blocking works on a Base plane.
Note that in the second and fourth example, the blocking piece lies in two planes,
only one of which is shown, and will cast a similar "shadow" on both planes.

Prince Appendix D - Illustrating Bishop and Scientist Moves:
On an open field, the Bishop may move to any space that shares any one dimension value with the Bishop,
and the change between the Bishop and the space in each of the other two dimensions is the same.
Remember that whenever "change" is used in this discussion, it may mean "amount added to" or "amount subtracted from" interchangeably.
A more mathematical way to refer to this would be "the absolute value of the difference."
The Scientist, again on an open field, may move to any space where,
when comparing the respective dimension values of the Scientist and the space, either:
Any one of the dimension values is the same, and the sum of the changes in the other two dimension values is even.
OR
There exists two dimension values where sum of the changes these two values is equal to the change of the third.
For you math and logic fans, here is another way of saying this:
Let the position value of a Scientist be the ordered triplet of dimension values (x,y,z),
and the position value of any other space be a similarly ordered triplet (i,j,k).
Furthermore, let these triplets be ordered in such a way that
|x - i| <= |y - j| <= |z - k|.
For simplicity of notation, also let
p = |x - i|, q = |y - j|, and r = |z - k|.
IF (p = 0 AND q + r is even) OR (p + q = r)
THEN the space is within the range of motion of the Scientist, assuming an open field.
Following is an illustration provided by L. Lynn Smith of the planes within which a Scientist may move
when placed in the middle of the field at Tier 4, Column 4, Row 4:

The Scientist move falls within seven different planes.
Three of these are the same planes within which a Base may move, although a Scientist is limited to a checkerboard pattern within these planes.
Two of these planes intersect along any line of Rook movement.
The other four planes fan out from the Scientist towards the corners of the field.
Two of these planes, along with one of the other three planes, intersect along any line of Bishop movement.
All planes intersect at the Scientist.
A destination space for a Scientist is blocked if space(s) occupied by other piece(s) exist(s) such that:
-For the dimension with the greatest change in value between the destination and the Scientist,
this dimension value is between the values of the destination and the Scientist.
-For the change in position value between both the space and the destination and the space and the Scientist,
the sum of the change in values of the other two dimensions is less than or equal to the change in value of the first dimension
(the dimension of greatest change in value between the destination and the Scientist).
-The piece is in the same plane as the destination.
-The destination is blocked in all planes it lies in.
If there is no single dimension of greatest change between the destination and the Scientist,
but instead two dimensions change by the same amount, with the third dimension not changing,
then one may arbitrarily consider either changing dimension as the dimension of greatest change.
For this to be the case, the destination must be along a line of a simple Bishop move, and can only be blocked by intervening pieces along this line.
The third condition is only an issue for destinations in the checkered Base planes.
For these planes, the piece is in the same plane as the destination
if the same dimension value that the Scientist and the destination share is also shared by the piece,
and the sum of the changes between the piece and the Scientist in the other two dimension values is even.
The last condition is only an issue for the destinations along the lines of Rook movement,
which lie in two checkered Base planes (and share two dimension values with the Scientist).
They may be blocked by two different pieces, one in each plane (with each sharing a different one of these two dimension values),
or a single piece along the same line of Rook movement that therefore lies in the same two planes
(and also shares the same two dimension values).
A math and logic formula of all this would look like this:
Let the position value of a Scientist be the ordered triplet of dimension values (x,y,z),
let the position value of any destination space be a similarly ordered triplet (i,j,k).
Furthermore, let these triplets be ordered in such a way that
|x - i| <= |y - j| <= |z - k|
Also let the position value of another space be a similarly ordered triplet (a,b,c).
Also let
p = |x - a|, q = |y - b|, and r = |z - c|.
And let
s = |a - i|, t = |b - j|, and u = |c - k|.
IF there is a piece occupying any space (a,b,c) such that
(z < c < k OR k < c < z)
AND (p + q <= r) AND (s + t <= u)
AND (IF x=i THEN [x=a AND q+r is even])
AND (IF y=j
THEN [y=b
OR {there is a piece occupying a space (d,e,f)
that satisfies the first two conditions (letting p = |x - d|, etc.)
AND y=e AND q+r is even}])
THEN the destination is blocked from the Scientist.
Below are illustrations of examples of blocking provided by L. Lynn Smith,
which I modified to indicate spaces which may be blocked depending on the other plane the space lies in (which is not shown).
Also note that in the 1st, 2nd, 4th, 6th, and 8th examples, the blocking piece also lies in other plane(s) not shown,
and will cast "shadows" on these plane(s) as well.
Appendix E - Illustrating the Merchant and Reporter Move
On an open field, the Merchant may move to any space where the change between the Merchant and the space in all dimension values is the same.
Remember again that whenever "change" is used in this discussion, it may mean "amount added to" or "amount subtracted from" interchangeably.
A more mathematical way to refer to this would be "the absolute value of the difference."
The Reporter, again on an open field, may move to any space where,
when comparing the respective dimension values of the Reporter and the space,
the change in any two of the dimension values is the same,
and the difference between this change and the change in the third dimension value is even
(remembering that zero is even and negative numbers may also be even).
Or, to say this with math and logic:
Let the position value of a Reporter be the ordered triplet of dimension values (x,y,z),
and the position value of any other space be a similarly ordered triplet (i,j,k).
For simplicity of notation, also let
p = |x - i|, q = |y - j|, and r = |z - k|.
IF
(p = q AND q - r is even)
OR (p = r AND p - q is even)
OR (q = r AND q - p is even)
THEN the space is within the range of motion of the Reporter, assuming an open field.
Following is an illustration provided by L. Lynn Smith of the planes within which a Reporter may move
when placed in the middle of the field at Tier 4, Column 4, Row 4:

The Reporter move falls within six different planes, each in a checkerboard, or "lace" pattern.
These planes fan out from the Reporter towards the edges of the field.
Two of these planes intersect along any line of Rook movement, three along any line of Merchant movement,
and all six intersect at the Reporter.
A destination space for a Reporter is blocked if space(s) occupied by other piece(s) exist(s) such that:
-It would be reachable in any number of moves by a Merchant starting where the Reporter is.
In other words, it shares the same relative "evenness" among the dimensions as the Reporter
(see Appendix A).
-For the dimension with the greatest change in value between the destination and the Reporter,
this dimension value is between the values of the destination and the Reporter.
-For the change in position value between both the piece and the destination and the piece and the Reporter,
the change in the dimension of greatest change between the destination and the Reporter
is greater than or equal to the change in values in each of the other two dimensions.
-The piece is in the same plane as the destination.
-The destination is blocked in all planes it lies in.
The fourth condition is only an issue if a destination has a single dimension of greatest change,
with the other two changing by the same (lesser) amount as each other.
The piece is in the same plane as the destination
if the two dimensions that change by the same amount between the Reporter and the destination
also change by the same amount between the Reporter and the piece,
and change the same way (add/subtract) relative to each other as they do between the Reporter and the destination.
For example: if they both add between the Reporter and the destination,
then they either both add or both subtract between the Reporter and the piece.
If these two dimensions do not change between the Reporter and the piece, then the piece is in the plane.
The last condition is only an issue with destinations along the lines of Rook movement, which lie within two planes.
In these cases, the two dimensions that change the same amount don't change at all.
These destinations may be blocked by two pieces where for one, these two dimensions change the same amount in the same way,
and for the other, these same two dimensions change the same amount in different ways (one adds, one subtracts).
These destinations may also be blocked by a single piece where both these dimensions also do not change,
meaning the piece is along the same line of Rook movement.
If there is no single dimension of greatest change between the destination and the Reporter,
but instead more than one dimension changes by the same amount, with any other dimension changing by less,
then one may arbitrarily consider any of the dimensions sharing the amount of greatest change as the dimension of greatest change.
A way to put this in math and logic would be:
Let the position value of a Reporter be the ordered triplet of dimension values (x,y,z),
let the position value of any destination space be a similarly ordered triplet (i,j,k).
Also let
m = |x - i|, n = |y - j|, o = |z - k|
Furthermore, let these triplets be ordered in such a way that
m <= n <= o
Also let the position value of another space within the Reporter's range of motion be a similarly ordered triplet (a,b,c).
Also let
p = |x - a|, q = |y - b|, and r = |z - c|.
And let
s = |a - i|, t = |b - j|, and u = |c - k|.
IF there is a piece occupying any space (a,b,c) such that
2*((a + b) MOD 2) + (a + c) MOD 2
= 2*((x + y) MOD 2) + (x + z) MOD 2
(see Appendix A)
AND ((z < c < k) OR (k < c < z))
AND (r>=p) AND (r>=q) AND (u>=s) AND (u>=t)
AND (IF o>n AND n <> 0
THEN [p=q AND (IF p <> 0
THEN [(x-i)*(y-j)/(m*n) =(x-a)*(y-b)/(p*q)])])
AND (IF n=0
THEN [{p=q AND p=0}
OR {there are two pieces occupying two spaces (a,b,c) and (d,e,f)
each of which satisfy the first two conditions (letting p=|x-a| or |x-d|, etc.)
AND p=q for each AND (x-a)*(y-b)/(|x-a|*|y-b|) <> (x-d)*(y-e)/(|x-d|*|y-e|)}])
THEN the destination is blocked from the Reporter by the piece.
Below are illustrations of examples of blocking provided by L. Lynn Smith,
which I modified to indicate spaces which may be blocked depending on the other plane the space lies in (which is not shown).
Also note that in all but the 1st example, the blocking piece also lies in other plane(s) not shown, and will cast "shadows" on these plane(s) as well.

Prince Appendix F - Quick Reference
The following is a quick reference for Prince put together by L. Lynn Smith.
It briefly describes how each kind of piece can move, as well as other basic rules of the game.
It is intended as a useful reference for when one actually tries to play Prince
so one doesn't have to keep everything about all 23 kinds of pieces in their head.
_____________________________________________________________________
Ace[Ac] leaps 2x3x3
Artist[Ar] slides diagonal or triagonal
Astronaut[As] leaps 1x2x3, 2x2x3 or 2x3x3
Admiral[Ad] leaps 2x2x3 or 2x3x3
Base[Ba] orthogonal planar area-leap
Bishop[Bi] slide diagonal
Captain[Ca] leaps 2x2x3
Court[Co] slide orthogonal or diagonal
King[Ki] steps orthogonal, diagonal or triagonal
May castle with directly diagonal Bases.
All castling rules apply.
Knight[Kn] leaps 1x2x3
Marine[Ma] leaps 1x2x3 or 2x2x3
Market[Mt] slides orthogonal or triagonal
Merchant[Me] slides triagonal
Network[Ne] orthogonal or triagonal planar area-leap
Paratrooper[Pa] leaps 1x2x3 or 2x3x3
Pawn[Pn] steps one forward orthogonal without capture,
steps one forward diagonal or forward triagoanl with capture.
May preform an initial two-step orthogonal move. En passant applies.
Freely promotes upon reach far rank.
Prince[Pr] orthogonal, diagonal or triagonal planar area-leap
Queen[Qu] slides orthogonal, diagonal or triagonal
Reporter[Re] triagonal planar area-leap
Rook[Ro] slides orthogonal
Scientist[Sc] diagonal planar area-leap
Spy[Sp] diagonal or triagonal planar area-leap
University[Un] orthogonal or diagonal planar area-leap
All pieces have the power to 'shadow' planar area-leaps.
Such planar area-leap may not move to cells which are 'shadow'-ed by other pieces.
Checkmate opposing King for win.

